Окружность - это геометрическая фигура, которая состоит из всех точек плоскости, равноудаленных от одной фиксированной точки, называемой центром окружности.
Иногда возникает необходимость узнать, принадлежит ли точка заданной окружности. Для этого нужно знать координаты центра окружности и радиус. Также необходимо знать координаты точки, которую нужно проверить.
Существует несколько способов определить принадлежность точки окружности по координатам:
1. Наиболее простым и понятным способом является вычисление расстояния между центром окружности и заданной точкой. Если расстояние меньше или равно радиусу, то точка принадлежит окружности. Формула для вычисления расстояния между двумя точками в плоскости: d = sqrt((x2 - x1)^2 + (y2 - y1)^2).
2. Также можно воспользоваться формулой для уравнения окружности: (x - a)^2 + (y - b)^2 = r^2, где (x, y) - координаты точки, (a, b) - координаты центра окружности, r - радиус. Если при подстановке координат заданной точки в это уравнение получается верное равенство, то точка принадлежит окружности.
Эти методы позволяют определить принадлежность точки окружности по координатам и использоваться в различных задачах, связанных с геометрией и программированием.
Определение принадлежности точки окружности
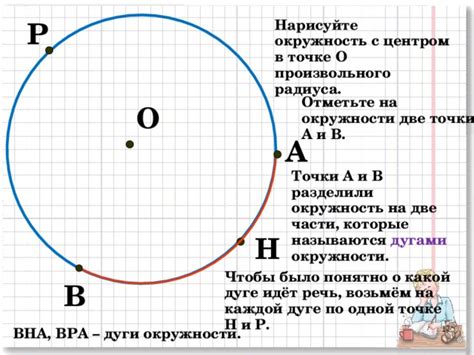
Когда нам нужно определить, принадлежит ли точка окружности или нет, мы можем использовать определение расстояния от точки до центра окружности. Для этого мы можем использовать формулу расстояния между двумя точками на плоскости:
Расстояние = √((x - cx)² + (y - cy)²)
Где (x, y) - координаты точки, cx и cy - координаты центра окружности.
Если расстояние от точки до центра окружности равно радиусу окружности, то точка лежит на окружности.
В противном случае, если расстояние меньше радиуса, то точка лежит внутри окружности. Если расстояние больше радиуса, то точка лежит вне окружности.
Для наглядности, можно использовать таблицу с примером:
| Точка (x, y) | Центр окружности (cx, cy) | Радиус окружности | Расстояние до центра | Принадлежность |
|---|---|---|---|---|
| (4, 5) | (3, 4) | 2 | √((4 - 3)² + (5 - 4)²) = √2 | Внутри |
| (1, 1) | (0, 0) | 3 | √((1 - 0)² + (1 - 0)²) = √2 | Вне |
| (0, 4) | (2, 2) | 4 | √((0 - 2)² + (4 - 2)²) = √8 | Внутри |
Исходя из вычисленного расстояния и радиуса, мы можем определить принадлежность точки окружности.
Понятие точки окружности

Координаты точки и радиус окружности
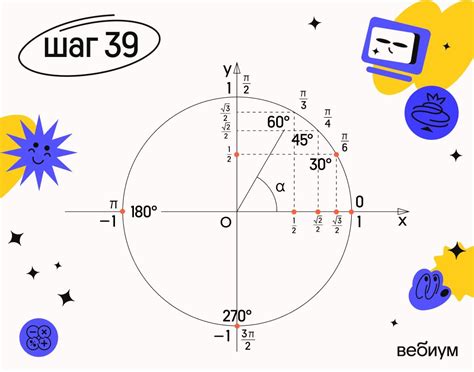
Координаты точки можно представить в виде пары чисел (x, y), где x – координата по горизонтали (ось Ox), y – координата по вертикали (ось Oy).
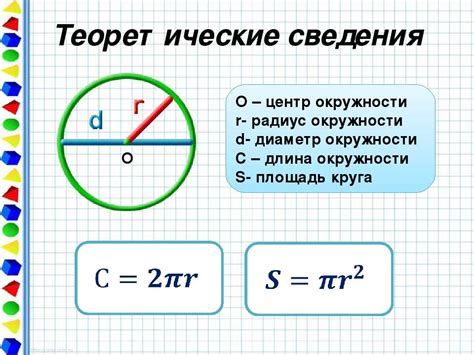
Радиус окружности – это расстояние от центра окружности до любой ее точки. Радиус обычно обозначается буквой R. Радиус окружности можно найти по формуле:
R = √((xц - x)2 + (yц - y)2)
где (xц, yц) – координаты центра окружности, (x, y) – координаты точки.
Для определения принадлежности точки к окружности необходимо сравнить расстояние от центра окружности до точки с радиусом окружности:
- Если расстояние равно радиусу окружности, то точка лежит на окружности.
- Если расстояние меньше радиуса окружности, то точка лежит внутри окружности.
- Если расстояние больше радиуса окружности, то точка лежит вне окружности.
В задачах на определение принадлежности точки окружности по координатам необходимо учесть эти условия.
Формула для определения принадлежности точки окружности
Для определения принадлежности точки окружности по ее координатам существует специальная формула, основанная на расстоянии между центром окружности и искомой точкой.
Формула выглядит следующим образом:
r = √((x - a)² + (y - b)²)
где:
- r - радиус окружности;
- x и y - координаты искомой точки;
- a и b - координаты центра окружности.
Если полученное значение r равно радиусу окружности, то искомая точка лежит на окружности. В противном случае, точка не принадлежит окружности.
Эта формула основана на теореме Пифагора, которая устанавливает связь между длинами сторон прямоугольного треугольника.
Использование этой формулы позволяет легко и быстро определить, принадлежит ли точка окружности, что может быть полезно в различных математических и графических задачах.
Примеры определения принадлежности точки окружности

Определение принадлежности точки окружности может быть выполнено с использованием различных методов. Рассмотрим несколько примеров:
- Метод расстояния. Для этого нужно найти расстояние от заданной точки до центра окружности. Если это расстояние равно радиусу окружности, то точка лежит на окружности. Если расстояние меньше радиуса, то точка находится внутри окружности, а если больше - снаружи.
- Метод уравнения окружности. Для этого задается уравнение окружности в виде (x - a)^2 + (y - b)^2 = r^2, где (a, b) - координаты центра окружности, r - радиус. Подставляем в уравнение координаты проверяемой точки и сравниваем результат с радиусом окружности. Если равенство выполняется, то точка лежит на окружности.
- Метод координатных плоскостей. Для этого задаются координаты проверяемой точки и центра окружности. Рассчитываются разности координат по каждой оси и сравниваются с радиусом. Если разности равны радиусу окружности, то точка лежит на окружности.
Каждый метод имеет свои преимущества и может быть использован для разных задач. Выбор метода зависит от требуемой точности, доступных вычислительных ресурсов и контекста, в котором задача решается.