Произведение двух чисел – это результат умножения их между собой. Обычно, когда у нас есть два числа и мы хотим найти их произведение, нам известны оба множителя. Однако иногда возникают ситуации, когда нам известен только один из множителей, а нужно найти значение второго. В этой статье мы рассмотрим несколько способов, как найти произведение с неизвестным вторым множителем.
Первый способ: воспользуемся свойством равенства произведения чисел. Если у нас есть произведение двух чисел и одно из них мы знаем, то мы можем найти второе число, деля произведение на известный множитель. Например, если мы знаем, что произведение двух чисел равно 20, а одно из чисел – 4, то мы можем найти второй множитель, разделив 20 на 4. Таким образом, второй множитель будет равен 5.
Второй способ: воспользуемся алгебраическим подходом. Предположим, что у нас есть уравнение, в котором один из множителей неизвестен, но мы знаем результат умножения. Мы можем записать это уравнение в виде произведения и привести его к стандартному виду, выражая неизвестный множитель через известный и результат умножения. Например, у нас есть уравнение 6x = 42. Мы знаем, что произведение 6 на неизвестный множитель x равно 42. Чтобы найти x, мы делим обе части уравнения на 6, и получаем x = 7.
Третий способ: используем метод перебора. Если нам известен результат умножения и одно из чисел, мы можем перебрать все возможные варианты для второго числа, пока не найдем подходящий. Например, если нам известно, что произведение двух чисел равно 15, а одно из чисел – 3, то мы начинаем перебирать варианты для второго числа: 1, 2, 3, 4, 5, и так далее. Когда мы дойдем до числа 5, мы увидим, что произведение 3 на 5 дает 15. Таким образом, второй множитель будет равен 5.
Методы нахождения произведения с неизвестным вторым множителем

Если у вас есть произведение двух чисел и известен один из множителей, а второй множитель предстоит найти, существует несколько методов, которые могут помочь решить эту задачу. Рассмотрим некоторые из них.
1. Метод подстановки
Данный метод подходит для случая, когда известно, что произведение двух чисел равно заданному числу. Для нахождения второго множителя можно последовательно подставлять различные значения, начиная от единицы, и проверять, равно ли произведение заданному числу. Когда будет найдено совпадение, найденное число будет являться вторым множителем.
2. Метод деления
Данный метод основан на том, что произведение двух чисел равно их умножению. Если известно, что произведение равно заданному числу, можно попробовать последовательно делить заданное число на различные значения и проверять, является ли результат целым числом. Когда будет найдено такое значение, найденное число будет вторым множителем.
3. Метод использования таблицы умножения
Данный метод основан на знании таблицы умножения. Если известен один из множителей и произведение, можно найти второй множитель, используя таблицу умножения. Необходимо найти число в строке с известным множителем и столбце с произведением, а это и будет искомым вторым множителем.
| Множитель 1 | Множитель 2 | Произведение |
|---|---|---|
| 1 | 2 | 2 |
| 1 | 3 | 3 |
| 1 | 4 | 4 |
| 2 | 1 | 2 |
| 2 | 2 | 4 |
| 2 | 3 | 6 |
Таким образом, существует несколько способов нахождения второго множителя, если известно произведение и один из множителей. Выбор метода зависит от конкретной ситуации и доступных исходных данных.
Разделение на множители

Для использования этого метода нужно знать, что произведение двух чисел равно их произведению. То есть, если a и b - два числа, и их произведение равно c, то можно записать уравнение: a * b = c.
Чтобы найти второй множитель, нужно разделить произведение на первый множитель. То есть, b = c / a.
Однако, стоит помнить, что этот метод работает только в случае, если первый множитель не равен нулю. Если первый множитель равен нулю, то произведение также будет равно нулю, и нельзя будет однозначно определить второй множитель.
Разделение на множители - это простой и эффективный способ нахождения второго множителя, когда известен результат произведения и один из множителей.
Расширенный алгоритм Евклида

Более формально, для двух чисел a и b расширенный алгоритм Евклида осуществляет следующие шаги:
- Инициализация: устанавливаются начальные значения a0 = a, b0 = b, x0 = 1, y0 = 0, x1 = 0, y1 = 1.
- Цикл: пока bn не станет равным нулю, выполняются следующие действия:
- Частное q = an-1 / bn-1 и остаток r = an-1 % bn-1 находятся с помощью деления с остатком.
- Обновление значений: an = bn-1, bn = r, xn = xn-2 - q * xn-1, yn = yn-2 - q * yn-1.
После завершения цикла значения an, xn и yn содержат НОД(a, b) и коэффициенты, удовлетворяющие следующему равенству: НОД(a, b) = an = xn * a + yn * b.
Расширенный алгоритм Евклида находит применение в различных областях, включая криптографию, теорию чисел и линейную алгебру. Он широко используется для решения задач, связанных с поиском обратного элемента по модулю, решением диофантовых уравнений и построением линейных комбинаций.
Использование арифметических свойств

При поиске произведения с неизвестным вторым множителем можно использовать арифметические свойства, такие как:
- Обратное свойство умножения: если произведение двух чисел равно заданному числу, то одно из множителей можно найти, разделив заданное число на другой множитель.
- Свойство коммутативности умножения: порядок множителей не влияет на произведение, поэтому при поиске произведения с неизвестным вторым множителем можно менять порядок множителей.
- Свойство ассоциативности умножения: скобки можно сократить, переместив множители в различные группы, поэтому при поиске произведения с неизвестным вторым множителем можно изменять расстановку скобок.
Использование этих свойств позволяет упростить задачу поиска произведения с неизвестным вторым множителем и найти результат более быстро и эффективно. Также, при работе с переменными, можно использовать алгебраические методы, такие как факторизация и раскрытие скобок, чтобы найти произведение. Важно помнить, что при использовании арифметических свойств необходимо проводить проверку полученного результата на корректность.
Применение формулы суммирования арифметической прогрессии

Формула суммирования арифметической прогрессии имеет следующий вид:
| Sn = (a1 + an) * n / 2 |
Где:
- Sn - сумма первых n элементов арифметической прогрессии;
- a1 - первый элемент арифметической прогрессии;
- an - n-й элемент арифметической прогрессии;
- n - количество элементов арифметической прогрессии.
Для нахождения произведения с неизвестным вторым множителем можно использовать формулу суммирования арифметической прогрессии, подставляя вместо суммы значение произведения и известные значения для первого множителя, первого элемента и количества элементов. Затем можно решить полученное уравнение для нахождения второго множителя.
Например, если известно, что произведение двух чисел равно 24, первый множитель равен 3, а количество элементов в арифметической прогрессии равно 4, то можно воспользоваться формулой суммирования арифметической прогрессии для нахождения второго множителя:
| 24 = (3 + a4) * 4 / 2 |
Решив это уравнение, мы найдем значение второго множителя и сможем найти произведение.
Таким образом, формула суммирования арифметической прогрессии может быть полезным инструментом для нахождения произведения с неизвестным вторым множителем в задачах, связанных с арифметическими прогрессиями.
Использование формулы ряда Гаусса

Для использования формулы ряда Гаусса нужно знать результат произведения двух чисел (произведение) и значение первого множителя. Формула выглядит следующим образом:
Произведение = Первый множитель * Второй множитель
Используя ряд Гаусса, мы можем переписать эту формулу в следующем виде:
Произведение = Первый множитель * (Первый множитель + 1) / 2
Теперь мы можем использовать эту формулу для нахождения значения второго множителя, зная только результат произведения и значение первого множителя.
Пример использования формулы ряда Гаусса:
- Значение первого множителя: 5
- Результат произведения: 20
Подставим значения в формулу и решим уравнение:
20 = 5 * (5 + 1) / 2
20 = 5 * 6 / 2
20 = 30 / 2
20 = 15
Таким образом, второй множитель равен 15.
Использование формулы ряда Гаусса позволяет нам эффективно находить значение второго множителя, когда нам известны результат произведения и значение первого множителя. Это может быть полезно при решении различных задач, связанных с поиском неизвестных значений в математике и физике.
Метод подбора

Шаги метода подбора:
- Определите известный множитель. Это число, с которым вы умножаете.
- Выберите различные значения для второго множителя и умножайте их на известный множитель.
- Проверяйте получившиеся произведения и сравнивайте их с данными о произведении. Если результат совпадает с неизвестным произведением, то значение второго множителя найдено.
Пример:
Задача:
Найдите второй множитель в произведении: 12 * ? = 72.
Шаги решения:
- Известный множитель: 12.
- Выбираем различные значения для второго множителя: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
- Проверяем получившиеся произведения: 12 * 1 = 12, 12 * 2 = 24, 12 * 3 = 36, 12 * 4 = 48, 12 * 5 = 60, 12 * 6 = 72. Результат совпадает с неизвестным произведением 72.
Таким образом, второй множитель в произведении 12 * ? = 72 равен 6.
Применение бинарного поиска
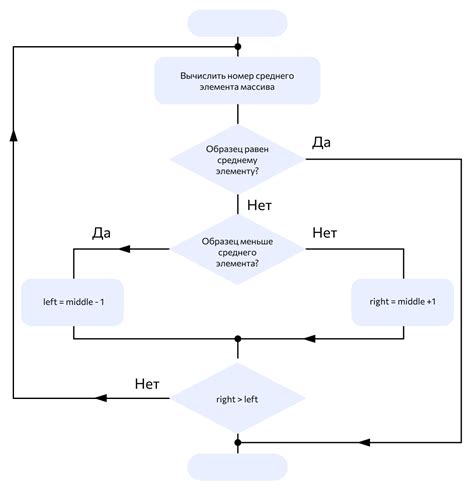
Применение бинарного поиска позволяет эффективно найти произведение с неизвестным вторым множителем, особенно когда известно, что это число находится в определенном диапазоне.
Бинарный поиск – это алгоритм, который использует деление отрезка пополам и сравнение искомого значения с серединой отрезка. Если значение больше середины, поиск продолжается в правой половине, иначе – в левой. Таким образом, поиск сокращается в два раза на каждой итерации.
Применяя этот алгоритм, можно быстро найти второй множитель, уменьшая диапазон поиска в два раза на каждой итерации. Начинается поиск с наименьшего возможного значения и заканчивается наибольшим возможным значением в данном диапазоне. Каждый раз, сравнивая произведение текущего значения с искомым числом, мы сужаем диапазон поиска до половины. Этот процесс повторяется до тех пор, пока не будет найдено искомое число или диапазон не будет сужен до одного значения.
Применение бинарного поиска позволяет максимально оптимизировать поиск второго множителя, особенно когда известно, что число находится в определенном диапазоне. Этот метод является эффективным и быстрым способом найти неизвестное значение в произведении.