Векторы - важная часть математики и физики. Они используются для представления физических величин, направлений и перемещений. Один из основных параметров вектора - его размер, или длина. Узнать размер вектора - это очень полезное умение, которое может пригодиться во многих областях жизни.
Для измерения длины вектора необходимо знать его координаты. Вектор представляет собой направленный отрезок, который можно задать числами. Координаты вектора указывают его начальную и конечную точки. Чтобы вычислить длину вектора, нужно использовать формулу, которая основана на теореме Пифагора.
Формула для вычисления длины вектора выглядит следующим образом:
|AB| = √((x₂ - x₁)² + (y₂ - y₁)²)
Где x₁, x₂ - координаты по оси X, y₁, y₂ - координаты по оси Y. Для трехмерных векторов формула немного сложнее, но основной принцип остается тот же - нужно вычислить разность между координатами точек и применить теорему Пифагора.
Итак, для вычисления размера вектора необходимо знать его координаты и использовать формулу с применением теоремы Пифагора. Таким образом, вы сможете определить длину вектора и использовать эту информацию в своей работе или в повседневной жизни.
Как понять размер вектора: шаги для измерения длины вектора
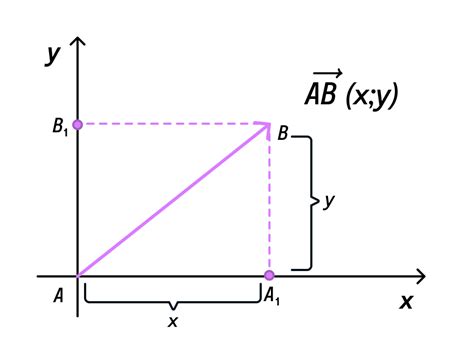
Шаг 2: Определите координаты начала и конца вектора. Начало вектора обозначается точкой (x1, y1), а конец вектора - точкой (x2, y2). Зная эти координаты, вы можете определить разницу между ними.
Шаг 3: Используйте формулу для измерения длины вектора. Длина вектора может быть определена с использованием теоремы Пифагора. Формула для расчета длины вектора выглядит следующим образом: