Треугольники являются одной из основных геометрических фигур, и их свойства изучаются уже на первом этапе обучения математике. Знание формул и правил, которые позволяют находить различные характеристики треугольников, является важным не только для решения математических задач, но и для понимания пространственных отношений в реальном мире.
Одним из таких важных параметров треугольников является их площадь. Площадь треугольника позволяет нам оценить, насколько он "занимает" поверхность, исчисливая площадную единицу, например, квадратный метр. Но что делать, если нам известны только стороны треугольника, а не его высота или углы? Как найти отношение площадей двух треугольников, имея на руках только значения их сторон? В этой статье мы рассмотрим инструкцию и приведем примеры расчета отношения площадей треугольников по известным сторонам.
Перед тем, как приступить к расчетам, необходимо освежить в памяти формулу для нахождения площади треугольника по его сторонам. Для этого существует формула Герона, которая позволяет найти площадь треугольника по полупериметру и длинам его сторон. По сути, формула Герона основана на применении теоремы Пифагора и представляет собой явное выражение для площади треугольника.
Дано:

Для решения задачи о нахождении отношения площадей треугольников по известным сторонам нам нужно знать следующие параметры:
- Длины сторон треугольников
- Формулу для вычисления площади треугольника
По известным сторонам треугольников можно использовать формулу Герона для вычисления площади. Формула Герона гласит:
S = √(p * (p - a) * (p - b) * (p - c)),
где S - площадь треугольника, a, b, c - длины сторон треугольника, p - полупериметр треугольника (p = (a + b + c)/2).
После вычисления площадей треугольников, можно вычислить отношение их площадей, разделив большую площадь на меньшую.
Инструкция

Если вам необходимо найти отношение площадей двух треугольников по известным сторонам, следуйте этим простым указаниям:
- Вспомните формулу площади треугольника: площадь треугольника равна половине произведения длины основания на высоту, опущенную на это основание.
- Измерьте длины оснований и высот для обоих треугольников.
- Примените формулу площади, чтобы найти площади обоих треугольников.
- Разделите площадь первого треугольника на площадь второго треугольника, чтобы получить отношение площадей.
Например, пусть у нас есть два треугольника. Первый треугольник имеет основание длиной 6 единиц и высоту 4 единицы, а второй треугольник имеет основание длиной 8 единиц и высоту 3 единицы. Первый треугольник будет иметь площадь 12 единицы, а второй треугольник будет иметь площадь 12 единиц. Отношение площадей будет 1:1.
Шаг 1: Найти полупериметр треугольника
Перед тем, как найти отношение площадей треугольников, необходимо найти полупериметр треугольника. Полупериметр (p) вычисляется по формуле:
p = (a + b + c) / 2
Где a, b и c - длины сторон треугольника.
Шаг 2: Найти площадь треугольника по формуле Герона
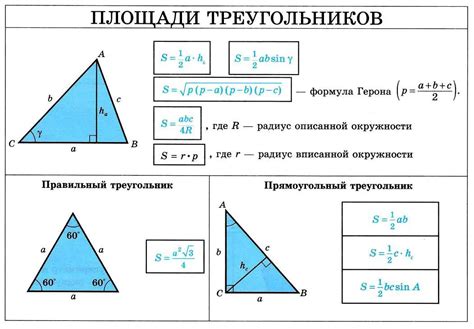
После того, как вы найдете длины всех сторон треугольника, вы можете найти его площадь с помощью формулы Герона. Формула Герона основывается на полупериметре треугольника (половина суммы длин всех его сторон) и длинах его сторон. Это удобный способ найти площадь треугольника, даже если у вас нет прямоугольного треугольника.
Формула Герона выглядит следующим образом:
S = √(p * (p - a) * (p - b) * (p - c))
где S - площадь треугольника, p - полупериметр треугольника, равный (a + b + c) / 2, а a, b и c - длины сторон треугольника.
Примените эту формулу, подставив значения длин сторон треугольника вместо соответствующих переменных. Вычислите значение под корнем и возьмите его квадратный корень, чтобы найти площадь треугольника.
Например, если у вас есть треугольник со сторонами a = 4, b = 5 и c = 6, сначала найдите полупериметр треугольника:
p = (a + b + c) / 2 = (4 + 5 + 6) / 2 = 15 / 2 = 7.5
Затем используйте полупериметр и значения сторон треугольника в формулу Герона:
S = √(7.5 * (7.5 - 4) * (7.5 - 5) * (7.5 - 6)) = √(7.5 * 3.5 * 2.5 * 1.5) = √(92.8125) ≈ 9.63
Таким образом, площадь треугольника с сторонами 4, 5 и 6 приближенно равна 9.63.
Шаг 3: Рассчитать отношение площадей треугольников

Чтобы рассчитать отношение площадей двух треугольников по известным сторонам, нужно использовать формулу герона для нахождения площади каждого треугольника. Затем полученные значения площадей нужно разделить друг на друга.
Давайте рассмотрим пример:
| Треугольник A | Треугольник B |
|---|---|
| Сторона AB: 5 | Сторона AB: 4 |
| Сторона AC: 7 | Сторона AC: 6 |
| Сторона BC: 8 | Сторона BC: 10 |
Для треугольника A:
Полупериметр (p) = (AB + AC + BC) / 2 = (5 + 7 + 8) / 2 = 20 / 2 = 10
Площадь (S) = √(p * (p - AB) * (p - AC) * (p - BC)) = √(10 * (10 - 5) * (10 - 7) * (10 - 8)) = √(10 * 5 * 3 * 2) = √(300) ≈ 17.32
Для треугольника B:
Полупериметр (p) = (AB + AC + BC) / 2 = (4 + 6 + 10) / 2 = 20 / 2 = 10
Площадь (S) = √(p * (p - AB) * (p - AC) * (p - BC)) = √(10 * (10 - 4) * (10 - 6) * (10 - 10)) = √(10 * 6 * 4 * 0) = √(0) = 0
Отношение площадей треугольников: SA / SB = 17.32 / 0 = undefined
В данном примере, так как площадь треугольника B равна нулю, отношение площадей треугольников не определено.
Важно отметить, что отношение площадей треугольников может быть положительным, отрицательным или равным нулю, и это зависит от конкретной ситуации и входных данных.
Примеры

Давайте рассмотрим несколько примеров для более полного понимания того, как найти отношение площадей треугольников.
Пример 1:
Допустим, у нас есть два треугольника со следующими сторонами:
Треугольник 1: сторона А = 5, сторона В = 8, сторона С = 10
Треугольник 2: сторона X = 6, сторона Y = 9, сторона Z = 12
Чтобы найти отношение площадей треугольников, мы должны сначала найти площади этих треугольников. Затем мы делим площадь одного треугольника на площадь другого треугольника.
Площадь треугольника 1 = √(s * (s - А) * (s - В) * (s - С)), где s - полупериметр треугольника, равный (А + В + С) / 2
Площадь треугольника 2 = √(s * (s - X) * (s - Y) * (s - Z)), где s - полупериметр треугольника, равный (X + Y + Z) / 2
Площадь треугольника 1 ≈ 19.81
Площадь треугольника 2 ≈ 24
Отношение площадей треугольников ≈ 19.81 / 24 ≈ 0.8254
Таким образом, отношение площадей треугольников будет около 0.8254.
Пример 2:
Рассмотрим два треугольника со следующими сторонами:
Треугольник 1: сторона А = 3, сторона В = 4, сторона С = 5
Треугольник 2: сторона X = 6, сторона Y = 8, сторона Z = 10
Площадь треугольника 1 = √(s * (s - А) * (s - В) * (s - С)), где s - полупериметр треугольника, равный (А + В + С) / 2
Площадь треугольника 2 = √(s * (s - X) * (s - Y) * (s - Z)), где s - полупериметр треугольника, равный (X + Y + Z) / 2
Площадь треугольника 1 ≈ 6
Площадь треугольника 2 ≈ 24
Отношение площадей треугольников ≈ 6 / 24 ≈ 0.25
Таким образом, отношение площадей треугольников будет около 0.25.
Пример 1: Нахождение отношения площадей треугольников с известными сторонами
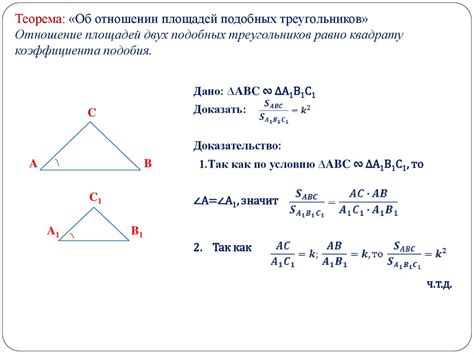
Задача: Даны два треугольника. Стороны первого треугольника равны 3, 4 и 5, а стороны второго треугольника равны 5, 12 и 13. Найти отношение площадей этих треугольников.
Решение:
Для нахождения отношения площадей треугольников, нужно сначала найти площади каждого треугольника, а затем поделить одну площадь на другую.
Площадь треугольника можно найти с помощью формулы Герона, где a, b и c - стороны треугольника:
Площадь треугольника:
S = sqrt(p * (p - a) * (p - b) * (p - c)),
где p - полупериметр треугольника: p = (a + b + c) / 2.
Площадь первого треугольника:
a = 3, b = 4, c = 5
p = (a + b + c) / 2 = (3 + 4 + 5) / 2 = 6
S1 = sqrt(p * (p - a) * (p - b) * (p - c)) = sqrt(6 * (6 - 3) * (6 - 4) * (6 - 5)) = 6
Площадь второго треугольника:
a = 5, b = 12, c = 13
p = (a + b + c) / 2 = (5 + 12 + 13) / 2 = 15
S2 = sqrt(p * (p - a) * (p - b) * (p - c)) = sqrt(15 * (15 - 5) * (15 - 12) * (15 - 13)) = 30
Отношение площадей:
S1 / S2 = 6 / 30 = 1 / 5
Ответ: Отношение площадей равно 1 / 5.