Обратная функция - это такая функция, которая связывает значения, полученные при заданной входной функции, с их исходными значениями. Другими словами, если функция f(x) присваивает каждому значению x значение f(x), то обратная функция f^(-1)(x) сопоставляет каждому значению x значение, которое было использовано как аргумент в исходной функции f(x).
Как определить, существует ли обратная функция? Для этого необходимо выполнение двух условий. Во-первых, функция должна быть взаимно однозначной, то есть каждому значению x из области определения функции должно соответствовать только одно значение y из области значений функции. Во-вторых, область определения функции должна быть равна области значений функции. Если оба этих условия выполняются, значит, обратная функция существует.
Кроме того, существует несколько признаков, по которым можно определить, является ли функция обратимой. Во-первых, обратная функция f^(-1)(x) существует только тогда, когда функция f(x) является взаимно однозначной. Это означает, что для любого значения x из области определения функции f(x) существует только одно значение y из области значений функции.
Определение понятия и существование обратной функции

Существование обратной функции зависит от того, является ли исходная функция инъективной (инъекция – свойство функции, при котором разным аргументам соответствуют разные значения). Если исходная функция является инъективной, то обратная функция существует и единственна.
- Если функция строго монотонно возрастает или строго монотонно убывает, то она является инъективной, и следовательно имеет обратную функцию.
- Если функция нестрого монотонна, то она может быть неинъективной и не иметь обратной функции. Например, функция y = x^2 не является инъективной и не имеет обратной функции.
Существование обратной функции можно проверить с помощью анализа первой производной функции и определения интервалов возрастания и убывания. Если функция удовлетворяет условию производной строго положительной или строго отрицательной, то существует обратная функция.
Обратная функция обозначается обычно буквой "f" с индексом "-1". Например, если у нас есть функция f(x), то ее обратная функция будет обозначаться f-1(x).
Понятие функции и ее обратной функции
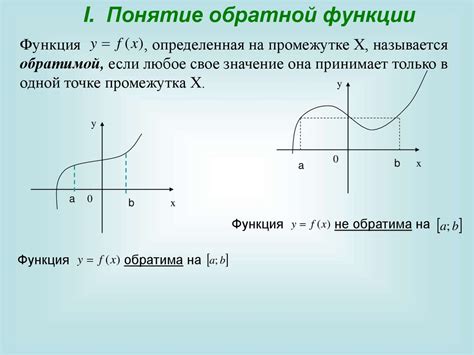
Функция представляет собой математическое понятие, которое устанавливает зависимость одного набора чисел, называемого доменом, от другого набора чисел, называемого областью значений. Функция может быть представлена в виде графика, табличной формы или алгебраического выражения.
Обратная функция - это функция, которая инвертирует зависимость между доменом и областью значений и позволяет найти исходное значение на основе полученного значения. То есть если у функции есть обратная функция, то можно восстановить исходные данные, зная результат.
Обратная функция обозначается обычно с помощью символа f^(-1), где f - исходная функция. Чтобы определить, существует ли обратная функция, необходимо проверить, является ли исходная функция биекцией. Биекция - это функция, которая является инъекцией (каждый элемент домена соответствует только одному элементу области значений) и сюръекцией (каждый элемент области значений имеет соответствующий элемент домена).
Если исходная функция является биекцией, то ее обратная функция существует и ее признаками являются:
- Домен обратной функции будет равен области значений исходной функции, и наоборот.
- Значения обратной функции будут соответствовать значениям исходной функции, и наоборот.
Обратная функция также может быть представлена в виде графика, табличной формы или алгебраического выражения.
Способы определения существования обратной функции

Первым способом определения существования обратной функции является изучение области определения и области значения функции. Если функция является биекцией, то есть каждому значению в области определения соответствует единственное значение в области значения, то обратная функция существует.
Второй способ заключается в анализе графика функции. Если график функции проходит тест вертикальной линии, где каждое горизонтальное сечение пересекает график только в одной точке, то функция является биекцией и имеет обратную функцию.
Третий способ состоит в проверке функции на монотонность. Если функция является строго монотонной, то есть либо строго возрастает, либо строго убывает, то она является биекцией и имеет обратную функцию.
Четвертый способ определения существования обратной функции основывается на анализе значения производной функции. Если производная функции нигде не обращается в ноль в области определения, то функция является монотонной и обратная функция существует.
Наконец, пятый способ заключается в проверке функции на инъективность. Если функция является инъективной, то есть каждому значению в области определения соответствует не более одного значения в области значения, то обратная функция существует.
Все эти способы помогают определить существование обратной функции и указывают на признаки, на которые нужно обратить внимание при анализе функции.
Признаки обратной функции
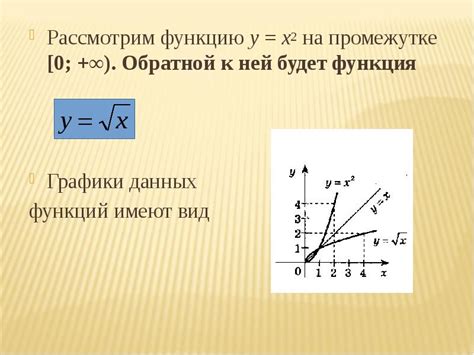
- Инъективность: исходная функция должна быть инъективной, то есть каждому аргументу функции должно соответствовать ровно одно значение.
- Сюръективность: исходная функция должна быть сюръективной, то есть для каждого значения функции должен существовать хотя бы один аргумент, которому оно соответствует.
- Ограниченность: функция должна быть ограничена на некотором интервале. Если функция стремится к бесконечности, то у нее не будет обратной функции.
Если один из этих признаков не выполняется, то обратная функция не существует или не является однозначной. Также стоит отметить, что обратная функция будет существовать только в определенном области определения исходной функции.