Вероятность - это одна из основных концепций, применяемых в математической статистике и теории вероятностей. Она позволяет оценить шансы на возможное событие или исход. Знание вероятностей может быть полезно в различных сферах жизни, от игр и спортивных ставок до научных исследований и предсказаний.
Для того чтобы найти вероятность, необходимо провести анализ и расчет на основе имеющихся данных. Существует несколько методов и формул, позволяющих определить вероятность события. Один из основных способов - это классическое определение вероятности. Оно основано на предположении о равномерности распределения исходов и определяется как отношение числа благоприятных исходов к общему числу исходов.
Еще одним методом расчета вероятности является статистический подход. Он основан на анализе статистических данных и определяет вероятность события на основе его частоты в определенной выборке. Для этого необходимо провести серию наблюдений или экспериментов и подсчитать количество раз, когда событие произошло, и относительную частоту его появления.
Как подсчитать вероятность: советы и методы расчёта

Существует несколько различных методов для расчета вероятности, каждый из которых подходит для определенных типов задач. От выбора подходящего метода зависит точность и надежность полученных результатов.
Одним из самых простых методов является классический подход. Он основан на предположении, что все исходы события равновероятны и не взаимосвязаны. Для расчета вероятности нужно определить число благоприятных исходов и разделить его на общее количество возможных исходов.
Если задача более сложная, можно использовать метод частотности или статистического подхода. Он основан на наблюдении за действительными данными и анализе статистической информации. Необходимо проследить за частотой возникновения события и использовать эти данные для расчета вероятности.
Вероятность также может быть вычислена с помощью математических моделей, таких как геометрические или алгебраические модели. Эти методы требуют глубоких знаний в математике и статистике, но обеспечивают высокую точность результатов.
Другим полезным инструментом при расчете вероятности является диаграмма Венна, которая позволяет визуализировать взаимосвязь различных исходов события. Диаграмма Венна помогает определить пересечение и объединение событий, что может быть полезным при расчете вероятности.
В конечном итоге, выбор метода расчета вероятности зависит от сложности задачи и доступных данных. Важно помнить, что точность и надежность результатов также зависят от качества входных данных и правильной интерпретации полученных результатов.
Расчет вероятности: основные понятия и определения

Элементарное событие – это событие, которое происходит в единственном эксперименте. Например, при броске монеты элементарными событиями будут выпадение "орла" или "решки".
Пространство элементарных событий – это множество всех возможных элементарных событий в эксперименте. Например, в случае броска монеты пространством элементарных событий будет множество {"орел", "решка"}.
Событие – это некоторое подмножество пространства элементарных событий. Оно может состоять из одного или нескольких элементарных событий. Например, событием при броске монеты может быть выпадение "орла".
Относительная вероятность – это вероятность события, выраженная в отношении числа благоприятных исходов данного события к числу всех возможных исходов. Относительная вероятность вычисляется с помощью формулы P(A) = m/n, где P(A) – вероятность события A, m – число благоприятных исходов, n – число всех возможных исходов.
Абсолютная вероятность – это вероятность события, выраженная в виде десятичной или процентной дроби. Она определяется путем сложения вероятностей всех элементарных событий, составляющих данное событие.
При расчете вероятности необходимо учитывать все факторы и условия, которые могут повлиять на наступление события. Использование математических методов и формул позволяет систематизировать и упорядочить процесс расчета вероятности.
Методы расчета вероятности событий

Вероятность события определяется как отношение числа благоприятных исходов к общему числу возможных исходов. Существуют различные методы расчета вероятности, которые могут быть применены в зависимости от характера события и имеющихся данных.
- Метод классической вероятности. Данный метод основан на том, что все исходы события равновероятны. Для его применения необходимо знать общее число исходов и число благоприятных исходов.
- Метод частотной вероятности. Этот метод основан на статистических данных и применяется в случаях, когда число исходов большое. Он основывается на опытном наблюдении за частотой появления события.
- Метод априорной вероятности. Этот метод применяется в случаях, когда имеется знание о вероятности событий, полученное до проведения опыта или установления данных.
- Метод условной вероятности. Этот метод используется в случаях, когда имеются дополнительные сведения о событии или других событиях.
Выбор метода расчета вероятности зависит от ситуации и доступных данных. Важно учитывать особенности события и иметь достаточное количество информации для корректного расчета. Более точные результаты можно получить при использовании дополнительных методов и при построении математических моделей.
Советы по расчету вероятности в различных ситуациях
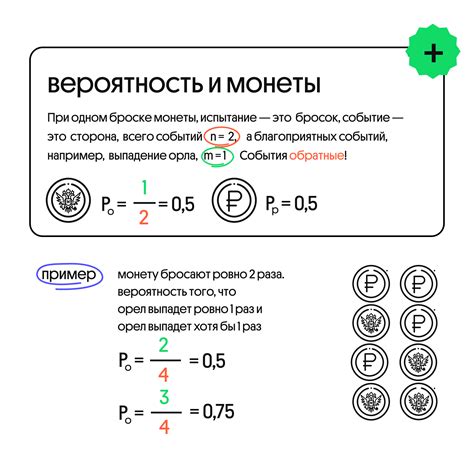
Расчет вероятности играет важную роль во многих областях, включая статистику, финансы, науку о данных и многие другие. В этом разделе мы разберем несколько советов по расчету вероятности в различных ситуациях.
1. Вероятность события как отношение числа благоприятных исходов к общему числу исходов: Если нам известно количество благоприятных исходов и общее количество возможных исходов, мы можем рассчитать вероятность события, разделив количество благоприятных исходов на общее количество исходов.
2. Вероятность суммы двух или более независимых событий: Если мы хотим рассчитать вероятность суммы двух или более независимых событий, мы можем умножить вероятности каждого события.
3. Вероятность события при наличии другого события: Если нам известна условная вероятность события A при наличии события B, то мы можем использовать формулу условной вероятности для расчета.
| Формула | Описание |
|---|---|
| P(A|B) = P(A и B) / P(B) | Формула условной вероятности |
4. Использование дерева возможных исходов: В некоторых случаях, особенно при расчете вероятности последовательных событий, можно использовать дерево возможных исходов для визуализации и расчета вероятности.
5. Получение данных и проведение экспериментов: В некоторых случаях, когда точные данные недоступны, можно использовать статистические методы для оценки вероятности. Это может включать проведение экспериментов, моделирование или использование базовых предположений.
Следуя этим советам, вы сможете более точно рассчитать вероятность в различных ситуациях и принять более обоснованные решения.
Примеры расчета вероятности событий
Как рассчитать вероятность того или иного события? Рассмотрим несколько примеров, чтобы понять, как применять методы расчета вероятности на практике.
Пример 1:
- Имеется урна с 5 разноцветными шариками: 2 красных, 2 синих и 1 желтый.
- Какова вероятность вытащить из урны красный шарик?
Решение:
- Сначала определяем общее количество возможных исходов – сумма всех шариков (5).
- Затем определяем количество благоприятных исходов – количество красных шариков (2).
- Вероятность вытащить красный шарик равна отношению благоприятных исходов к общему количеству исходов: 2/5 = 0,4 или 40%.
Пример 2:
- В колоде карт (52 карты) имеется 4 туза.
- Какова вероятность вытянуть туз, если карту вытаскивают наугад?
Решение:
- Сначала определяем общее количество возможных исходов – количество карт в колоде (52).
- Затем определяем количество благоприятных исходов – количество тузов (4).
- Вероятность вытянуть туз равна отношению благоприятных исходов к общему количеству исходов: 4/52 ≈ 0,077 или около 7,7%.
Пример 3:
- Из 20 человек, 13 говорят по-английски, 7 – по-французски, 4 – и по-английски, и по-французски.
- Какова вероятность выбрать человека, который говорит хотя бы на одном из этих языков?
Решение:
- Сначала определяем общее количество возможных исходов – количество людей (20).
- Затем определяем количество благоприятных исходов – количество людей, говорящих хотя бы на одном из языков (13 + 7 - 4 = 16).
- Вероятность выбрать такого человека равна отношению благоприятных исходов к общему количеству исходов: 16/20 = 0,8 или 80%.
Таким образом, расчет вероятности событий может быть достаточно простым, если знать количество благоприятных и исходов и использовать соответствующую формулу.