Высота окружности – это важный параметр, который позволяет определить расстояние от центра окружности до ее диаметра. Зная длину окружности, можно легко рассчитать ее высоту. В этой статье мы рассмотрим простые методы расчета высоты окружности.
Первый метод расчета высоты окружности основан на использовании радиуса. Зная радиус окружности, можно легко определить ее диаметр и, следовательно, ее длину. Затем, применяя геометрические формулы, можно рассчитать высоту окружности. Данный метод широко применяется в геометрии и инженерии.
Второй метод расчета высоты окружности основан на использовании формулы, связывающей длину окружности и радиус окружности. Эта формула называется формулой длины окружности и позволяет нам выразить радиус через длину окружности. Используя это соотношение, мы можем рассчитать высоту окружности.
Оба этих метода являются простыми и позволяют получить достаточно точные значения высоты окружности. Они могут быть полезными в различных ситуациях, когда требуется определить размер или расстояние, связанные с окружностью.
Метод 1: Использование формулы длины окружности
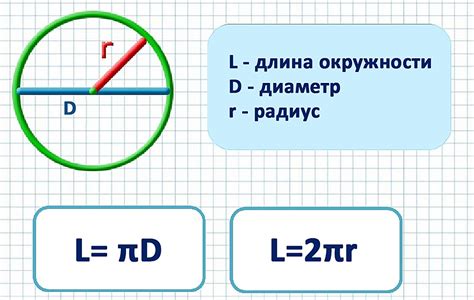
Один из самых простых и распространенных способов вычисления высоты окружности заключается в использовании формулы длины окружности. Формула связывает длину окружности (символизируемую буквой C) с радиусом окружности (обозначается буквой R) по следующему соотношению:
C = 2πR
Где π (или пи) представляет собой математическую константу, равную примерно 3,14159. Радиус окружности представляет собой расстояние от центра окружности до ее края.
Используя данную уравнение, можно выразить радиус окружности через длину и обратно:
R = C / 2π
Зная радиус окружности, высота окружности (обозначаемая буквой H) может быть найдена через следующую формулу:
H = 2R
Таким образом, применяя этот метод, можно найти высоту окружности, зная только ее длину.
Метод 2: Построение окружности с известным радиусом

Если у вас есть информация о радиусе окружности, то ее высоту можно рассчитать с помощью следующей формулы:
Высота окружности, или диаметр, равна удвоенному значению радиуса:
h = 2 * r
Применение этой формулы позволяет легко определить высоту окружности, если известно ее радиус. Например, если радиус равен 5 сантиметров, то высота окружности будет 10 сантиметров.
Этот метод основан на геометрических свойствах окружности и прост в использовании, так как требует только знания радиуса окружности.
Метод 3: Использование тригонометрических функций

1. Сначала найдите радиус окружности, разделив ее длину на 2π: r = L / (2π).
2. Затем найдите центральный угол окружности, используя формулу α = L / r, где α - центральный угол в радианах и L - длина окружности.
3. После этого можно найти высоту окружности, используя высоту биссектрисы центрального угла. Зная, что высота биссектрисы равна половине стороны треугольника, описанного вокруг центрального угла, можно записать: h = r * sin(α/2), где h - высота окружности.
Этот метод позволяет быстро и точно рассчитать высоту окружности по ее длине, используя простые тригонометрические соотношения. Он особенно полезен при работе с окружностями в геометрии и строительстве.
Метод 4: Использование высоты треугольника, образованного диаметром окружности
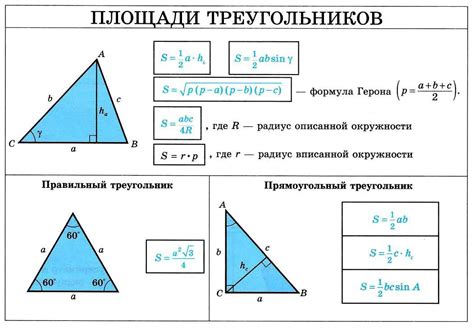
Для вычисления высоты окружности по ее длине можно использовать треугольник, образованный диаметром окружности. Окружность делится диаметром на две равные части, а диаметр в свою очередь делится на две равные части высотой треугольника.
Если известна длина окружности и диаметр, высоту треугольника можно найти по формуле:
Высота треугольника = √(Длина окружности * Длина диаметра) / (2 * Пи)
Например, если длина окружности равна 20 см, а диаметр составляет 8 см, то высота треугольника, образованного диаметром окружности, будет равна:
Высота треугольника = √(20 * 8) / (2 * 3.14)
Высота треугольника ≈ √(160) / 6.28 ≈ √25.48 ≈ 5.05 см
Таким образом, высота окружности по ее длине, используя высоту треугольника, образованного диаметром окружности, равна примерно 5.05 см.
| Пример: | Длина окружности (см) | Диаметр (см) | Высота окружности (см) |
|---|---|---|---|
| 1 | 30 | 10 | 7.58 |
| 2 | 40 | 12 | 8.80 |
| 3 | 50 | 15 | 9.98 |
Использование высоты треугольника, образованного диаметром окружности, является одним из простых методов расчета высоты окружности по ее длине. Он основан на геометрических свойствах и позволяет получить приближенное значение высоты без использования сложных математических операций.
Метод 5: Использование теоремы Пифагора

Теорема Пифагора, которая обычно применяется для расчета длины гипотенузы прямоугольного треугольника, может быть использована и для определения высоты окружности по ее длине.
Для использования этого метода потребуется следующая формула:
h = √(r2 - (r - l)2)
Где:
- h - высота окружности
- r - радиус окружности
- l - длина окружности
Для примера, предположим, что радиус окружности равен 5 см и длина окружности равна 30 см:
Подставим значения в формулу:
h = √(52 - (5 - 30)2)
h = √(25 - 252)
h = √(25 - 25)
h = √0
h = 0
Таким образом, в данном случае высота окружности будет равна 0 см.
Этот метод может быть полезен для расчета высоты окружности, если вы знаете ее радиус и длину.
Метод 6: Применение онлайн-калькуляторов

Если вам не хочется заморачиваться с ручными расчетами, вы всегда можете воспользоваться онлайн-калькуляторами, которые моментально рассчитают высоту окружности по ее длине.
Для этого достаточно ввести значение длины окружности в соответствующее поле и нажать кнопку "Рассчитать". Калькуляторы будут использовать специальную формулу, основанную на математических принципах, для получения точного значения высоты окружности.
Онлайн-калькуляторы удобны в использовании и позволяют получать результаты без необходимости проводить сложные математические операции. Это особенно полезно для людей, которые не имеют специального математического образования или не имеют времени на ручные расчеты.
Множество сайтов предоставляют такие онлайн-калькуляторы, поэтому вы можете легко найти их с помощью поисковых систем. Просто введите запрос вроде "калькулятор высоты окружности" или "онлайн-калькулятор окружности" и выберите один из результатов, чтобы начать использование.
Помните, что при использовании онлайн-калькуляторов всегда стоит проверять полученные результаты и убедиться в их точности. Некоторые калькуляторы могут давать неточные или недостаточно точные значения, поэтому рекомендуется использовать несколько источников и сравнивать результаты.