В математике, дроби играют важную роль при выполнении операций с числами. Правильные дроби - это дроби, в которых числитель меньше знаменателя. Понимание правильности дробей основополагающее для различных аспектов математики, физики, экономики и многих других областей науки и приложений.
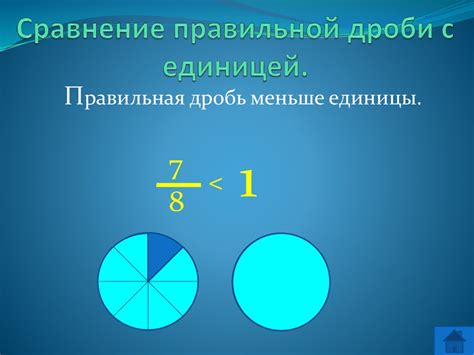
Для определения правильности дроби достаточно сравнить числитель и знаменатель. Если числитель меньше знаменателя, то дробь считается правильной. Например, в дроби 2/3 числитель равен 2, а знаменатель равен 3. Поскольку 2 меньше 3, дробь 2/3 является правильной.
Правильные дроби могут быть простыми или составными. Простые дроби - это дроби, у которых числитель является простым числом и не имеет общих делителей с знаменателем, кроме 1. Например, дробь 3/4 является простой, так как числитель 3 - простое число и не имеет общих делителей с знаменателем 4. Составные дроби, в свою очередь, имеют числитель, который может быть разложен на более маленькие простые числа и/или имеют общие делители с знаменателем. Например, дробь 6/8 является составной, так как числитель 6 может быть разложен на простые числа 2 и 3, а знаменатель 8 имеет общий делитель 2 с числителем.
Что такое правильная дробь?

Например, дробь 1/2 является правильной, потому что числитель (1) меньше знаменателя (2) и значение дроби равно 0.5, что находится в диапазоне от 0 до 1.
Для определения, является ли дробь правильной, нужно сравнить числитель и знаменатель. Если числитель меньше знаменателя, то дробь считается правильной.
Правильные дроби могут быть использованы для представления долей и десятичных дробей. Они могут быть приведены к десятичному виду или использованы в арифметических операциях, таких как сложение, вычитание, умножение и деление.
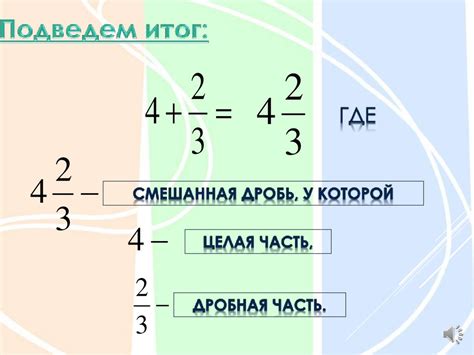
Обратите внимание, что существуют также неправильные дроби и смешанные числа. Неправильная дробь имеет числитель, который больше знаменателя, тогда как смешанное число представляет собой комбинацию целой части и дробной части (например, 1 1/2).
Понятие правильной дроби
Для определения того, является ли дробь правильной, необходимо сравнить числитель и знаменатель.
Если числитель меньше знаменателя, то дробь будет правильной. Например, 2/5, 3/4 и 7/10 - все эти дроби являются правильными.
Основное свойство правильной дроби заключается в том, что она представляет только часть целого числа. Например, дробь 3/4 означает, что у нас есть только 3 части из 4 возможных, а 1/2 означает, что у нас есть только половина от целого.
Правильные дроби могут использоваться для представления долей и процентов. Например, если мы имеем дробь 2/3, это означает, что у нас есть 2 части от возможных 3, что соответствует приблизительному значению 66,67 процента.
Правильные дроби являются важным понятием в математике и широко используются в повседневной жизни для представления долей и доли числовых значений.
Определение правильной дроби
Правильные дроби можно представить в виде десятичной дроби, которая будет иметь значение меньше 1. Например, дробь 3/4 в десятичной форме будет равна 0.75, что меньше 1.
Другие примеры правильных дробей:
- 1/2
- 2/3
- 5/8
Правильные дроби часто используются для представления долей от целого числа. Например, если у вас есть 8 яблок, и вы съели 3 из них, то можно представить это в виде дроби 3/8, где числитель (3) - это количество съеденных яблок, а знаменатель (8) - общее количество яблок.
Определение правильной дроби важно для понимания и работы с дробными числами. Правильные дроби имеют свои особенности и свойства, которые помогают в решении уравнений и задач, связанных с долями, процентами и долями от целого.
Как определить, является ли дробь правильной?

Если числитель и знаменатель равны, то такая дробь называется единичной. Например, 4/4 является единичной дробью.
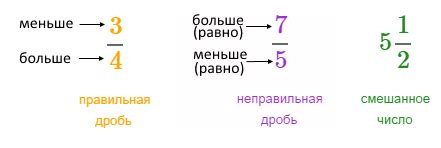
Если числитель больше знаменателя, то дробь называется неправильной. Например, дробь 5/2 является неправильной, так как 5 больше 2.
Иногда может быть полезно привести неправильную дробь к смешанной. Смешанная дробь состоит из целой части и обыкновенной дроби, например, 3 1/2. Это означает, что у нас есть 3 целых части и 1/2 обыкновенная дробь.
Знание, как определить, является ли дробь правильной, полезно при работе с дробями и выполнении арифметических операций с ними.
Итак, чтобы определить, является ли дробь правильной, просто сравните числитель и знаменатель. Если числитель меньше знаменателя, дробь является правильной.
Примеры правильных дробей

Вот несколько примеров правильных дробей:
- 1/2 - одна вторая
- 3/4 - три четверти
- 2/3 - две третьих
- 5/8 - пять восьмых
- 7/10 - семь десятых
В этих примерах числитель (верхняя часть дроби) меньше знаменателя (нижняя часть дроби), что делает дроби правильными. Все эти дроби могут быть представлены в виде конечных десятичных дробей или периодических десятичных дробей.
Что делать, если дробь неправильная?

Если дробь неправильная, то это означает, что числитель больше знаменателя. Например, в дроби 5/3, числитель равен 5, а знаменатель равен 3.
Чтобы привести неправильную дробь к правильному виду, необходимо выполнить деление числителя на знаменатель и получить целую часть и остаток. Например, дробь 5/3 можно привести к правильному виду следующим образом:
5 ÷ 3 = 1 целая часть и 2/3 остаток.
Таким образом, неправильная дробь 5/3 можно записать как смешанную дробь 1 2/3.
Приведение неправильной дроби к правильному виду особенно полезно при работе с дробями в математических операциях, таких как сложение, вычитание, умножение и деление. Правильная дробь легче выполнять математические операции, т.к. она имеет целую часть и остаток.
Как привести неправильную дробь к правильной?

- Разделите числитель на знаменатель. Полученное целое число будет являться целой частью правильной дроби.
- Оставшийся остаток после деления будет использован в качестве числителя для новой дроби.
- Знаменатель правильной дроби остается тем же, что и у исходной неправильной дроби.
Например, рассмотрим неправильную дробь 7/4:
- 7 ÷ 4 = 1 (целая часть правильной дроби)
- 7 % 4 = 3 (остаток, который будет использован в качестве числителя для новой дроби)
Таким образом, неправильная дробь 7/4 может быть приведена к правильной дроби 1 3/4.
Приведение неправильных дробей к правильным позволяет более удобно выполнять арифметические операции и сравнения с другими дробями.
Пример приведения неправильной дроби к правильной
Для приведения неправильной дроби к правильной, необходимо разделить числитель на знаменатель и записать остаток в виде смешанной дроби.
Рассмотрим пример: дробь 7/4.
| Неправильная дробь | Операция | Окончательный результат |
|---|---|---|
| 7/4 | Деление числителя на знаменатель: 7 ÷ 4 = 1 | 1 3/4 |
Таким образом, неправильная дробь 7/4 была приведена к правильной дроби 1 3/4.