Определение значения переменной b на графике функции может быть важной задачей в математике. Зная значение b, мы можем получить полное уравнение функции и точно описать ее поведение. Однако иногда по графику может быть непросто определить значение b, особенно если он находится вне области видимости или представляет собой число с десятыми или сотыми долями.
Существует простой способ определить значение b по графику функции. Перед вами стоит задача найти точку на графике, в которой функция пересекает ось ординат (ось y). Значение точки пересечения и будет являться значением переменной b. Заметим, что особенность данного способа заключается в том, что нам необходимо рассмотреть только одну точку, тем самым избегая сложных вычислений.
Для выполнения данного метода необходимо обратиться к графику функции и отметить точку пересечения с осью ординат. Если график пересекает ось ординат в точке с координатами (0, b), то значение переменной b равно y-координате данной точки. Применение этого метода не требует использования формул или специальных решений, поэтому он является простым и эффективным.
Определение значения b по графику функции: простой способ
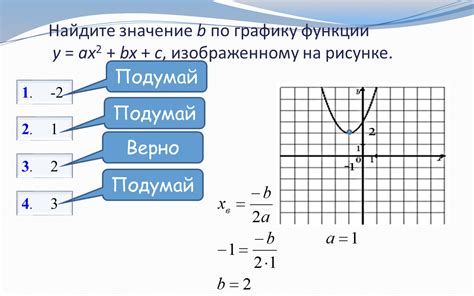
Простейший способ определить значение b по графику функции состоит в анализе точек пересечения графика с осью OY (осью ординат).
Для определения значения b нужно найти точку, в которой график функции пересекает ось OY. Это обозначает, что значение функции в этой точке равно нулю. Основываясь на этом, можно составить уравнение:
f(x) = ax + b = 0,
где f(x) - значение функции в точке x,
a - значение наклона графика функции.
Решив уравнение, можно найти значение b:
b = -a * x,
где x - координата точки пересечения графика с осью OY.
Таким образом, простым способом определения значения b по графику функции является нахождение точки пересечения с осью OY и подстановка полученных координат в уравнение.
Шаг 1: Изучение графика функции
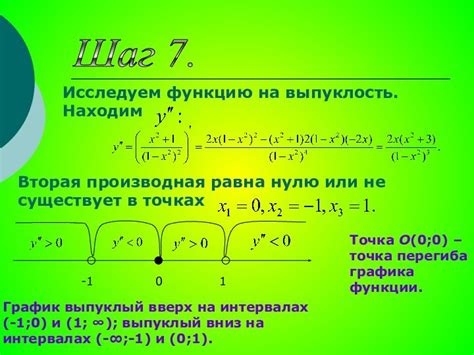
Перед тем, как определить значение переменной б по графику функции, необходимо внимательно изучить сам график. График функции представляет собой визуальное отображение зависимости между значениями переменных в функции.
Первым шагом в изучении графика функции является определение основных особенностей: точек пересечения с осями координат, экстремумов, точек разрыва и асимптот. Также важно обратить внимание на области возрастания и убывания функции.
После этого необходимо определить значения функции для нескольких известных точек на графике. Для этого можно использовать координаты наименее и наиболее ярко выраженных точек графика. Например, можно выбрать a, b и с точки, которые легко определить на основе внешнего вида графика функции.
Запомнив значения функции для выбранных точек, можно использовать их для определения значения переменной б по графику функции. Например, если известно, что значение функции при x=a равно у1, а при x=b равно у2, то можно составить уравнение:
у1 = a + б
у2 = b + б
С помощью этих уравнений можно найти значение переменной б. Для решения подобных уравнений можно использовать различные методы, например, метод подстановки или метод исключения.
Таким образом, первым шагом в определении значения переменной б по графику функции является тщательное изучение графика функции, определение его особенностей и значений функции для нескольких известных точек. Затем можно использовать полученные значения для составления и решения уравнений и определения значения переменной б.
Шаг 2: Определение точки пересечения графика с осью ординат
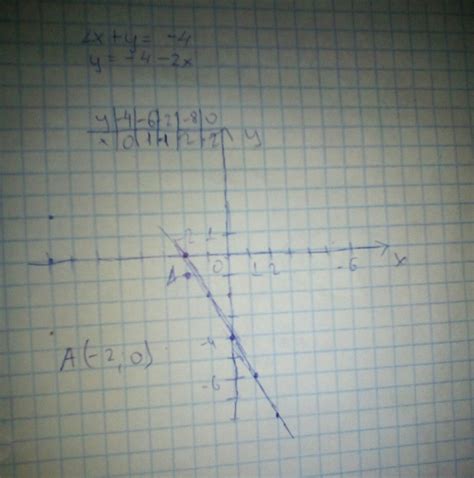
Для определения точки пересечения с осью ординат, нужно обратить внимание на точку, в которой график функции пересекает данную ось. Обычно это точка, в которой график функции пересекает линию ординат. Ордината обозначает ось, расположенную вертикально на плоскости координат.
Чтобы определить координаты точки пересечения, необходимо найти значение функции в этой точке. Для этого следует обратить внимание на значение функции по вертикальной оси на пересечении с горизонтальной осью x. Значение функции в точке пересечения с осью ординат будет являться искомым значением б, которое нужно найти.
Таким образом, шаг определения точки пересечения графика функции с осью ординат основан на нахождении значения функции в точке пересечения с горизонтальной осью x. Значение функции в этой точке будет координатой точки пересечения с осью ординат и искомым значением б.