Решение уравнений - это одно из основных математических навыков, которому учат детей уже с 5 класса. Чтобы научиться решать уравнения, необходимо понять, как найти значение переменной. Это навык, который всегда пригодится в повседневной жизни и в дальнейшем, поэтому важно усвоить его правильно.
Чтобы найти значение переменной в уравнении, необходимо следовать нескольким шагам. Во-первых, нужно перенести все слагаемые с переменной на одну сторону уравнения, а все числа - на другую. Для этого используют принцип "равенство", который позволяет сделать одинаковые преобразования с обеими сторонами уравнения.
После переноса слагаемых с переменной на одну сторону, необходимо перенести все числа на другую сторону. Для этого используют принцип "противоположность", который позволяет изменить знак числа на противоположный. В результате получается уравнение, в котором слева остается только переменная, а справа - число.
Для нахождения значения переменной необходимо разделить число справа на коэффициент перед переменной слева. Полученное значение и будет ответом на уравнение. Не забывайте, что нахождение значения переменной - это всего лишь часть решения, и необходимо всегда проверять его, подставляя полученное значение переменной в исходное уравнение.
Как найти значение переменной в уравнении

Для того чтобы найти значение переменной в уравнении, необходимо использовать основные принципы алгебры. В алгебре переменные обозначаются буквами и представляют неизвестные значения. Чтобы решить уравнение и определить значение переменной, необходимо использовать различные операции и правила алгебры.
Первый шаг в поиске значения переменной - это избавиться от скобок и упрощения выражения. Для этого следует применить коммутативное, ассоциативное и дистрибутивное свойства операций.
Затем следует использовать правила решения уравнений, такие как свойства равенства и преобразования выражений. Оперируя с обеими сторонами уравнения, можно последовательно совершать действия, чтобы избавиться от переменной и найти ее значение.
Необходимо помнить, что действия, которые применяют к одной стороне уравнения, необходимо также применять и к другой стороне, чтобы уравнение оставалось равным.
Например, если у нас есть уравнение 2x + 4 = 10, то мы можем изначально избавиться от скобок, вычитая 4 из обеих сторон уравнения:
2x + 4 - 4 = 10 - 4
2x = 6
Затем мы можем разделить обе стороны уравнения на 2, чтобы найти значение x:
2x / 2 = 6 / 2
x = 3
Таким образом, значение переменной x в уравнении 2x + 4 = 10 равно 3.
Итак, чтобы найти значение переменной в уравнении, необходимо применять различные математические операции и правила алгебры, чтобы постепенно избавиться от переменной и найти ее значение.
Методы решения одночлена с одной неизвестной
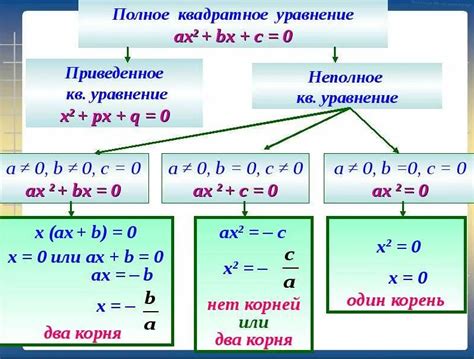
Существует несколько методов решения одночлена:
1. Метод подстановки: для этого метода необходимо подставить различные значения переменной и проверить, при каком из них выражение станет верным. Например, если у нас есть одночлен 2x-3=7, мы можем подставить значения x равные 2, 3, 4 и так далее, и проверить, при каком из этих значений выражение будет равно 7.
2. Метод баланса: в этом методе необходимо свести одночлен к виду, где переменная остается сама по себе. Например, если у нас есть одночлен 3x+4=13, мы можем перенести все числа вправо и получить 3x=9. Затем делим обе части уравнения на коэффициент перед переменной 3 и получаем x=3.
| Метод | Пример | Решение |
|---|---|---|
| Метод подстановки | 2x-3=7 | x=5 |
| Метод баланса | 3x+4=13 | x=3 |
Таким образом, зная различные методы решения одночлена с одной неизвестной, ученики 5 класса могут эффективно находить значения переменной в уравнении и решать математические задачи.
Решение уравнений с одной переменной

Для начала необходимо определить тип уравнения. Наиболее простым типом является уравнение вида "a + x = b", где "a" и "b" - известные числа, а "x" - неизвестное значение, которое необходимо найти.
Для решения данного уравнения нужно избавиться от слагаемого "a" на одной стороне уравнения, перенося его на другую сторону с заменой знака на противоположный:
| a + x = b | (-a) |
| x = b - a |
Таким образом, значение переменной "x" будет равно разности чисел "b" и "a".
Обратите внимание, что того же самого результата можно достичь, если к обеим сторонам уравнения добавить или вычесть одно и то же число, чтобы избавиться от слагаемого на одной из сторон.
Решение уравнений с одной переменной может быть более сложным, если вместо сложения и вычитания требуется использовать умножение и деление. В таком случае необходимо применять соответствующие математические операции для нахождения значения переменной.
Важно помнить, что решение уравнений с одной переменной - это процесс, в результате которого находится одно корректное значение, удовлетворяющее условию уравнения. Если уравнение имеет более одного решения или не имеет решений вообще, то в этом случае следует провести дополнительные рассуждения или использовать другие методы решения уравнений.
Как избавиться от скобок в уравнении

Скобки в уравнениях могут создавать путаницу и запутывать, поэтому их необходимо удалить, чтобы упростить решение задачи. Вот несколько методов, которые помогут избавиться от скобок.
1. Раскрытие скобок: Если в уравнении есть скобки, их можно раскрыть, перемножив каждый элемент внутри скобок на каждый элемент снаружи скобок. Например: (2 + 3) * 4 = 2 * 4 + 3 * 4 = 8 + 12 = 20.
2. Использование распределительного закона: Если в уравнении есть скобки с разными операциями (сложение и умножение), можно использовать распределительный закон для упрощения. Например: 2 * (3 + 4) = 2 * 3 + 2 * 4 = 6 + 8 = 14.
3. Обратное распределение: Если в уравнении есть одинаковые элементы в скобках, их можно вынести за скобки, используя знак сложения или вычитания. Например: 2 * (3 + 4) = 2 * 3 + 2 * 4 = 6 + 8 = 14.
4. Применение алгебраических свойств: В некоторых случаях можно использовать алгебраические свойства, чтобы избавиться от скобок. Например, закон коммутативности позволяет изменять порядок слагаемых в скобках, закон ассоциативности позволяет изменять порядок операций внутри скобок.
Используя эти методы, вы сможете избавиться от скобок в уравнении и упростить его решение.
Однако, нужно помнить, что порядок действий в уравнении необходимо соблюдать, чтобы получить правильный ответ.
Решение уравнений с двумя переменными

Уравнения с двумя переменными представляют собой уравнения, в которых присутствуют две неизвестных величины. Их решение позволяет найти значения обеих переменных, удовлетворяющие заданному равенству.
Для решения таких уравнений нужно использовать методы алгебры, включая применение законов эквивалентных преобразований. Один из эффективных способов решения двух переменных - метод подстановки. В этом методе используется представление одной переменной через другую и последующая подстановка этого значения в другое уравнение.
Найденное значение переменной можно проверить, подставив его в исходное уравнение. Если равенство сохраняется, то полученное значение является корректным решением уравнения.
Некоторые уравнения с двумя переменными могут иметь неограниченное количество решений или решений в виде графика на координатной плоскости. В таких случаях, для решения уравнений нужно использовать графические методы, такие как построение линий и их пересечение.
Важно помнить, что решение уравнений с двумя переменными требует аккуратности и внимательности. Рекомендуется использовать упражнения и примеры для закрепления знаний и практики решения таких уравнений.
Знание и понимание методов решения уравнений с двумя переменными поможет ученикам 5 класса развить свои навыки алгебры и подготовиться к более сложным математическим задачам в будущем.
Задачи на решение уравнений

- У Маши было 5 яблок, и она съела неизвестное количество яблок. В результате у нее осталось 2 яблока. Сколько яблок Маша съела? Решите уравнение 5 - х = 2.
- На полке стояло некоторое количество книг, и Миша добавил на полку еще несколько книг. Теперь на полке стало 8 книг. Сколько книг Миша добавил? Решите уравнение х + 4 = 8.
- В мешке было несколько марок монет. Яна положила еще 3 монеты в мешок, и в итоге в мешке стало 9 монет. Сколько монет было изначально в мешке? Решите уравнение х + 3 = 9.
Все эти задачи можно решить, применяя принцип, что чтобы найти значение переменной, нужно противопоставить две стороны уравнения и выполнить необходимые операции.
Помните, что решение уравнений требует от вас внимательности и точности. Постарайтесь использовать эти задачи для тренировки и улучшения навыков в решении уравнений. Удачи вам!
Практические примеры по решению уравнений

Пример 1:
Решите уравнение: 2x + 5 = 15
Решение:
Для того чтобы найти значение переменной x, нужно сначала избавиться от постоянной части уравнения. Вычтем 5 из обеих сторон:
2x + 5 - 5 = 15 - 5
2x = 10
Затем разделим обе стороны на коэффициент при x:
2x / 2 = 10 / 2
x = 5
Ответ: x = 5
Пример 2:
Решите уравнение: 3y - 7 = 8
Решение:
Также, чтобы найти значение переменной y, нужно избавиться от постоянной части уравнения. Прибавим 7 к обеим сторонам:
3y - 7 + 7 = 8 + 7
3y = 15
Затем разделим обе стороны на коэффициент при y:
3y / 3 = 15 / 3
y = 5
Ответ: y = 5
Применение этих методов к различным примерам позволит вам легко находить значения переменных в уравнениях и успешно решать задачи. Для лучшего понимания материала регулярно практикуйтесь и решайте больше уравнений!