Амплитуда является одним из важных параметров при анализе и измерении колебаний и волн. Она показывает максимальное отклонение системы от равновесного положения. Найти амплитуду формулы можно с помощью нескольких простых шагов, используя знания о функциях и графиках. Это позволяет с легкостью определить величину колебаний и их интенсивность.
Сначала необходимо иметь формулу, описывающую колебания или волну. Например, для гармонического движения формула может быть представлена как y(t) = A*sin(wt + phi), где A - амплитуда, w - угловая частота, t - время, phi - начальная фаза. В этой формуле амплитуда A показывает максимальное отклонение частицы от равновесного положения.
Чтобы найти амплитуду, необходимо построить график функции y(t) и найти точку, в которой достигается максимальное отклонение. На графике амплитуда соответствует вертикальной линии, которая проходит через эту точку. Можно использовать программы для построения графиков или ручные методы, чтобы визуализировать функцию и найти амплитуду.
Что такое амплитуда и как ее найти?

Для нахождения амплитуды необходимо обратиться к соответствующей формуле в зависимости от типа колебательного процесса:
- Для гармонического колебания амплитуда может быть найдена по формуле A = |xmax − xmin| / 2, где xmax и xmin - максимальное и минимальное положения точки соответственно. Результат будет выражен в тех же единицах, что и величина, измеряемая колебательным процессом.
- Для амплитудно-фазового модулированного сигнала амплитуда определяется как максимальное значение огибающей. В данном случае, амплитуда измеряется в вольтах или аналогичных единицах.
- Для амплитудной модуляции амплитуду можно найти путем измерения максимального значения полезного сигнала (например, аудиосигнала).
Знание амплитуды позволяет оценить интенсивность колебательного процесса и применять различные методы для его измерения и анализа.
Амплитуда: определение и примеры
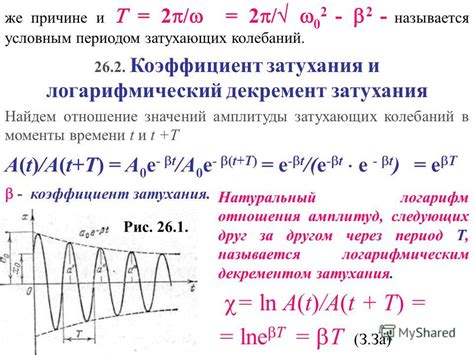
В физике амплитуда обычно применяется для измерения максимальной амплитуды колебаний. Например, при описании гармонических колебаний, амплитуда соответствует максимальному удалению колеблющейся точки от положения равновесия. Она определяется численно и обычно измеряется в метрах (м) или любых других единицах измерения, соответствующих конкретному направлению колебаний.
Амплитуда также может быть применена в других областях, например, в звуковой технике. В этом случае амплитуда относится к изменению акустического давления в звуковой волне. Высота звукового сигнала и громкость зависят от его амплитуды. Чем больше амплитуда звуковой волны, тем громче звук.
Другим примером применения амплитуды является измерение электрических сигналов. В электронике амплитуда сигнала отражает изменение напряжения или тока во времени. Это важная характеристика, которая может указывать на мощность и эффективность электрической схемы или устройства.
Таким образом, амплитуда является важным параметром для характеристики различных типов сигналов и колебаний. Она позволяет определить максимальное отклонение от среднего значения и имеет значительное значение во многих научных и технических приложениях.
Как рассчитать амплитуду?

Для расчета амплитуды вам понадобится информация о переменной величине и периоде колебания. Если у вас есть график изменения величины во времени, амплитуду можно найти, измерив расстояние от нулевой точки до максимальной точки волны или колебания.
Формула для расчета амплитуды выглядит следующим образом:
Амплитуда = (Максимальное значение - Минимальное значение) / 2
Вычитая минимальное значение из максимального и деля результат на 2, мы получаем половину разницы между этими значениями, что и является амплитудой.
Не забывайте, что амплитуда всегда положительна, поскольку измеряется как расстояние от нуля до максимальной точки колебания. Если величина изменяется только по отрицательной оси, вы можете просто взять модуль полученного значения амплитуды.
Важно отметить, что формула для расчета амплитуды может различаться в зависимости от типа волны или колебания, с которым вы работаете. Например, для синусоидальной волны амплитуда равна половине амплитуды выборки между максимальной и минимальной точкой волны.
Расчет амплитуды может быть полезным для многих приложений, включая изучение звуковых волн, электромагнитных полей, механических колебаний и других физических явлений. Он позволяет количественно измерить интенсивность волны или колебания и получить информацию о их свойствах и характеристиках.
Формула для расчета амплитуды
Формула для расчета амплитуды зависит от типа колебания или волны. В случае гармонического колебания, амплитуду можно расчитать по следующей формуле:
А = A0 * cos(ωt + ϕ)
где:
- А - амплитуда;
- A0 - максимальное значение колебаний;
- ω - угловая частота колебаний;
- t - время;
- ϕ - начальная фаза колебаний.
Для других типов колебаний или волн могут быть использованы разные формулы для расчета амплитуды. Например, для стоячей волны на струне или в трубе можно использовать формулу:
А = 2A0
где А0 - амплитуда отдельных волн стоячей волны.
Простое объяснение расчета амплитуды
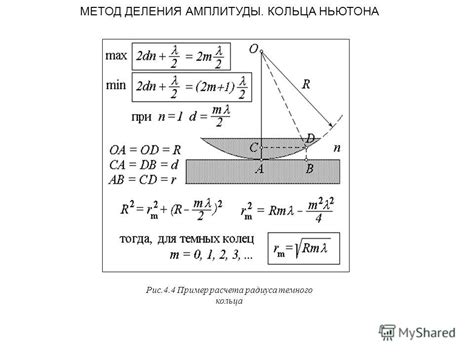
Для расчета амплитуды необходимо знать две величины: максимальное значение сигнала и среднее значение сигнала. Максимальное значение сигнала представляет максимальное смещение от среднего значения, а среднее значение - среднее арифметическое всех значений сигнала за период времени.
Для простоты объяснения, представим, что имеется гармоническое колебание, описываемое синусоидальной функцией sin(t). Амплитуда этого колебания будет равна абсолютному значению максимального смещения от нулевого значения функции sin(t).
Например, если максимальное значение сигнала sin(t) равно 5, а его среднее значение равно 0, то амплитуда будет равна 5.
В общем виде, амплитуду можно вычислить с помощью следующей формулы:
Амплитуда = (Максимальное значение сигнала - Среднее значение сигнала) / 2
Таким образом, расчет амплитуды включает определение максимального значения сигнала и его среднего значения, а затем применение формулы для вычисления амплитуды. Этот простой подход позволяет получить точную величину амплитуды и использовать ее для анализа сигналов и колебаний в различных областях науки и техники.
Примеры расчета амплитуды
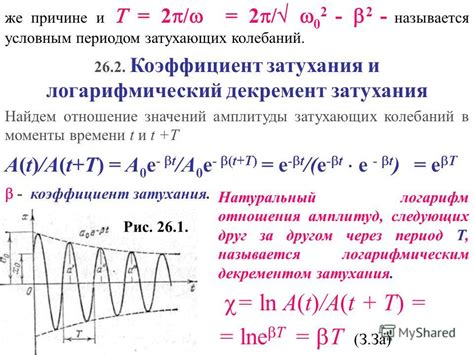
Расчет амплитуды может быть осуществлен для различных величин и явлений. Ниже представлены несколько примеров расчета амплитуды для различных случаев.
Пример 1: Расчет амплитуды звуковой волны.
| Параметр | Значение |
|---|---|
| Давление максимальной точки | 2 Па |
| Давление минимальной точки | 1 Па |
| Амплитуда | 1 Па |
Пример 2: Расчет амплитуды электрического сигнала.
| Параметр | Значение |
|---|---|
| Максимальное напряжение | 5 В |
| Минимальное напряжение | 0 В |
| Амплитуда | 5 В |
Пример 3: Расчет амплитуды колебаний механического объекта.
| Параметр | Значение |
|---|---|
| Максимальное смещение | 10 м |
| Минимальное смещение | 0 м |
| Амплитуда | 10 м |
В каждом из приведенных примеров амплитуда вычисляется как разность между максимальным и минимальным значениями соответствующей величины. Расчет амплитуды позволяет определить максимальное изменение параметра в процессе колебаний или сигнала и является важным показателем при анализе различных физических явлений.
Амплитуда и ее значение в различных областях
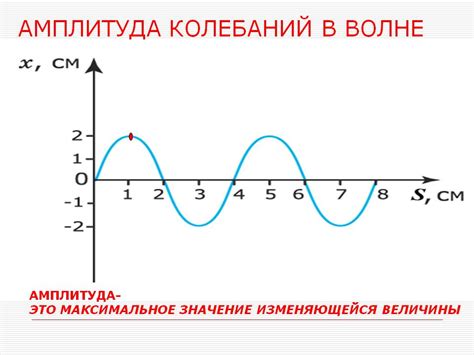
В физике амплитуда описывает максимальное значение колебаний или величину переменного процесса. В механике, например, амплитуда относится к расстоянию от положения равновесия до крайнего положения колеблющегося объекта. Чем больше амплитуда, тем сильнее колебания.
В электродинамике амплитуда указывает на максимальное значение электрического сигнала, такого как напряжение или ток. Для звуковых волн амплитуда соответствует громкости звука.
В оптике амплитуда световой волны определяет яркость или интенсивность света. Чем больше амплитуда световой волны, тем больше его интенсивность. Амплитуда также может влиять на цвет света, где большая амплитуда соответствует более яркому цвету, а меньшая - менее яркому.
В цифровой обработке сигналов, амплитуда определяет максимальное значение сигнала на заданном временном интервале. Это может быть полезно при анализе звуковых сигналов или изображений.
Таким образом, амплитуда имеет важное значение во многих областях, от физики до электроники и обработки сигналов. Понимание амплитуды помогает описать и анализировать различные явления и процессы в разных науках и технических областях.