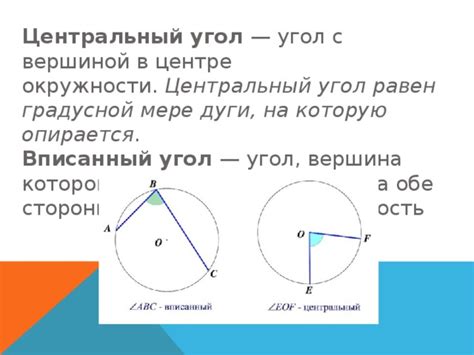
Центральный угол по дуге это угол, образованный двумя лучами, исходящими из центра окружности и соединяющими его с концами этой дуги. Этот тип угла часто используется в геометрии и может быть полезен при решении различных задач. Если вас интересует, как найти центральный угол по дуге, то вам понадобятся определенные знания и навыки.
Для начала, вам нужно знать длину дуги и радиус окружности. Эти два параметра абсолютно необходимы для расчета центрального угла. Поскольку центральный угол зависит от длины дуги и радиуса, имеет смысл использовать формулу для нахождения угла по длине дуги, которая выглядит следующим образом:
Угол = (Длина дуги / Радиус) * 180 / π
Где π является математической константой, близкой к значению 3.14159. Вы можете использовать это значение или примерное значение для более точных результатов. Как только вы найдете угол в градусах, вы сможете продолжить использовать его для решения задачи, для которой вам нужно было найти центральный угол по дуге.
Важно отметить, что в некоторых случаях вам может потребоваться использовать другие формулы или методы для нахождения центрального угла по дуге. В зависимости от конкретной задачи и имеющихся данных, вам может потребоваться более сложный подход. В таких случаях полезно обратиться к специалистам или использовать специализированные ресурсы для решения вашей проблемы.
Как найти центральный угол по дуге

Для начала, найдите радиус окружности. Радиус - это расстояние от центра окружности до любой точки на ней. Измерьте это расстояние с помощью линейки или другого подходящего инструмента.
Далее, измерьте длину дуги, для которой вы хотите найти центральный угол. Можно использовать специальные измерительные инструменты, такие как гониометр, или просто измерить длину дуги с помощью линейки и перевести ее в соответствующую единицу измерения (например, градусы).
Используя найденные значения радиуса и длины дуги, вы можете вычислить центральный угол с помощью следующей формулы:
Угол = (длина дуги / радиус) * 180° / π
Где π (пи) - это математическая константа, приближенное значение которой составляет около 3.14. Ответ будет выражен в градусах.
Теперь, когда вы знаете, как найти центральный угол по дуге, вы можете применить этот подход в решении различных задач геометрии. Удачи в ваших изысканиях и путешествиях по миру математики!
Определение центрального угла и его важность

Определение центрального угла имеет большую важность в геометрии. Этот угол позволяет нам измерить и описать свойства фигур на окружности. Например, центральный угол может служить инструментом для определения длины дуги окружности или нахождения площади сегмента окружности.
Центральные углы также играют важную роль в тригонометрии и векторном анализе. Они позволяют определить ориентацию и направление в пространстве, а также рассчитать величину и направление векторов.
Понимание определения и свойств центральных углов позволяет нам более глубоко изучать и применять геометрию и математику в реальных задачах и практических примерах, что делает их изучение необходимым и полезным для любого учащегося или профессионала в сфере науки и техники.
Методы нахождения центрального угла по дуге
| Метод | Описание |
|---|---|
| Метод радиуса | Данный метод основан на свойстве центрального угла, согласно которому наполовину дуги, соответствующей центральному углу, равны мере этого угла в градусах. |
| Метод сектора | Этот метод основан на свойстве центрального угла, согласно которому отношение меры сегмента, ограниченного дугой и сторонами центрального угла, к длине окружности равно отношению меры центрального угла к 360 градусам. |
| Метод дуги | Данный метод применяется, когда дуга является частью большей дуги и необходимо найти центральный угол, ограниченный данной дугой. Для этого нужно использовать свойство пропорциональности между мерой дуги и мерой центрального угла. |
| Метод тригонометрии | Этот метод использует тригонометрические функции синуса, косинуса и тангенса для нахождения меры центрального угла по дуге. |
Выбор метода нахождения центрального угла по дуге зависит от конкретной задачи и доступных данных. Каждый из перечисленных методов имеет свои особенности и может быть эффективным в определенных ситуациях. Использование таблицы методов поможет выбрать наиболее подходящий способ решения задачи.
Применение центрального угла в практике

Одним из основных применений центрального угла является вычисление длин дуги. Дуга окружности – это фрагмент окружности между двумя точками. Для вычисления длины дуги необходимо знать центральный угол. Пусть дана окружность с радиусом R и центральный угол α (в радианах). Тогда длина дуги L вычисляется по формуле:
L = Rα
Другим важным применением центрального угла является нахождение площади сектора окружности. Сектор – это фрагмент окружности, ограниченный двумя радиусами и дугой. Для вычисления площади сектора необходимо знать центральный угол и радиусы. Пусть дана окружность с радиусом R и центральный угол α (в радианах). Тогда площадь S сектора вычисляется по формуле:
S = (πR^2 * α) / 2π = R^2 * α / 2
Кроме того, центральный угол применяется в различных задачах геометрии и механики. Например, он используется для решения задач на построение или определение взаимного расположения геометрических фигур. Знание центрального угла позволяет провести необходимые вычисления и принять рациональные решения в практических задачах.
Использование центрального угла в практике позволяет анализировать и работать с окружностями и их частями. Это значительно облегчает решение задач и позволяет применять геометрические знания на практике.