Дроби – это числа, которые состоят из двух частей: числителя и знаменателя. Однако, иногда нам может потребоваться найти только дробную часть от целого числа. Это может быть полезно, например, при округлении переменных или в финансовых расчетах. В этой статье мы рассмотрим несколько простых способов вычисления части дроби от целого числа.
Первый способ – использование арифметических операций для нахождения дробной части числа. Для этого нужно разделить число на знаменатель и получить остаток от деления. Например, если у нас есть число 7 и мы хотим найти его дробную часть из 3, то мы делим 7 на 3 и получаем остаток 1.
Однако, существует и более короткий способ найти часть дроби от целого числа, используя только операцию остатка от деления. Для этого нужно использовать оператор % (процент) в языках программирования или функцию MOD в Microsoft Excel. Например, если мы хотим найти часть дроби от числа 7 из 3, мы можем записать 7 % 3 и получим результат 1.
В конечном итоге, независимо от способа, который вы используете, вы всегда сможете найти часть дроби от целого числа. Этот навык может оказаться полезным во многих сферах жизни, начиная от математических вычислений до программирования и финансовых расчетов.
Понимание понятия "часть дроби"
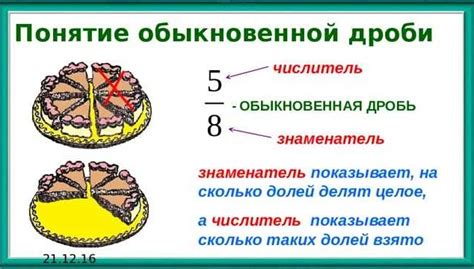
Понятие "часть дроби" связано с понятием дроби в математике. Дробь состоит из двух чисел: числителя и знаменателя, например, 3/4. Числитель указывает, сколько частей целого мы имеем, а знаменатель показывает, на сколько частей мы разделили целое число.
Часть дроби от целого числа выражает, сколько целых частей есть в дроби. Например, для дроби 3/4, часть дроби от числа 5 будет равна 3, так как в 5 поместится 4 целых части дроби.
Для нахождения части дроби от целого числа нужно разделить это число на знаменатель дроби. Например, для дроби 3/4 и числа 5:
- 5 ÷ 4 = 1 с остатком 1
Определенная часть дроби будет равна частному, то есть 1.
Другой способ нахождения части дроби от целого числа - это умножить числитель дроби на целое число и разделить полученное произведение на знаменатель. Например, для дроби 3/4 и числа 5:
- 3 × 5 = 15
- 15 ÷ 4 = 3 с остатком 3
Определенная часть дроби будет равна частному, то есть 3.
Зная, как найти часть дроби от целого числа, вы можете использовать этот метод, чтобы решать различные математические задачи и применять его в повседневной жизни.
Что такое часть дроби и как она связана с целым числом?

Частью дроби называется числовое значение после запятой в десятичной записи числа. Это значение указывает, какая часть от целого числа представляет собой дробная часть числа.
Часто в математических задачах возникает необходимость вычислить часть дроби от целого числа. Например, при решении задачи о распределении чего-либо поровну на несколько частей. В таких случаях важно понимать, какая часть из целого числа представляет собой дробную часть и как ее выразить в виде десятичной или обыкновенной дроби.
Связь между частью дроби и целым числом очевидна - они образуют вместе исходное значение числа. Находя часть дроби от целого числа, мы получаем информацию о том, сколько единиц из исходного числа составляет дробная часть. Это является важным элементом для понимания и использования дробных значений.
Есть несколько способов нахождения части дроби от целого числа. Один из самых распространенных методов - деление. Он основан на том, что часть дроби получается при делении целого числа на определенное значение. Другой метод - использование математических операций, таких как умножение и вычитание. Важно понимать, что каждый из этих методов имеет свои особенности и подходит для разных ситуаций.
Как найти часть дроби от целого числа

Чтобы найти часть дроби от целого числа, следуйте следующим шагам:
- Определите значение дробного числа. Например, если у вас есть дробное число 5.75, то целая часть равна 5, а дробная - 0.75.
- Игнорируйте целую часть числа. В данном примере число 5 будет игнорироваться.
- Запишите десятичную дробь без целой части. В данном примере десятичная дробь будет равна 0.75.
Теперь у вас есть часть дроби от целого числа. В данном примере часть дроби от числа 5.75 составляет 0.75.
Найденная часть дроби может быть использована для дальнейших вычислений или анализа данных. В математике и финансовых расчетах, знание части дроби от целого числа может быть полезно для округления чисел, проведения статистических анализов или определения доли процента.
Запомните, что часть дроби от целого числа представляет собой дробную часть числа, исключая целую часть. Следуя простым шагам, вы сможете легко найти эту часть и использовать ее для решения задач в различных областях.
Советы по нахождению части дроби от целого числа

При решении задач, связанных с нахождением части дроби от целого числа, полезно придерживаться следующих советов:
1. Определите дробную часть числа: для этого вычитайте целую часть числа из самого числа. Например, для числа 5.75 дробная часть равна 0.75.
2. Используйте десятичную форму: приведите дробную часть числа к десятичной форме, если она еще не является десятичной. Например, дробь 3/4 равна 0.75.
3. Представьте дробную часть в процентном виде: умножьте десятичную форму дробной части на 100, чтобы представить ее в процентах. Например, 0.75 дробной части будет соответствовать 75%.
4. Примените полученное значение: используйте полученное процентное значение для решения соответствующей задачи или для выполнения необходимых дальнейших вычислений.
Следуя этим советам, вы сможете более эффективно находить часть дроби от целого числа и применять это знание в различных контекстах.
Примеры вычисления части дроби от целого числа

Если вы хотите узнать, как найти часть дроби от целого числа, вам необходимо использовать определенную формулу. Ниже приведены несколько примеров, которые помогут вам лучше разобраться в этом процессе:
- Пример 1: Пусть у нас есть дробное число 6.75. Чтобы найти часть дроби от этого числа, вычтите из него его целую часть. В данном случае, целая часть равна 6, поэтому результат будет равен 0.75.
- Пример 2: Рассмотрим число 4.25. Целая часть этого числа равна 4, поэтому часть дроби будет равна 0.25.
- Пример 3: Допустим, у нас есть число 8.5. Вычитаем целую часть 8 из этого числа и получаем 0.5 в качестве части дроби.
Таким образом, найдя разницу между дробным числом и его целой частью, мы получаем часть дроби от целого числа. Это очень полезно во многих математических и научных задачах, а также при работе с дробными числами в программировании и финансовых расчетах.