Диаметр шара – одна из важнейших характеристик этого геометрического тела. Он определяется как двукратное значение радиуса, и знание диаметра помогает в различных расчетах. Но как узнать диаметр по радиусу? Простой математический прием поможет нам справиться с этой задачей.
Воспользуемся формулой: Диаметр = 2 * Радиус. То есть, чтобы найти диаметр шара, нужно умножить значение радиуса на 2. Например, если радиус равен 5 сантиметрам, то диаметр будет равен 10 сантиметрам. Это легкое правило поможет вам получить точный результат без особых математических умений.
Расчет диаметра шара по радиусу применяется в различных сферах, таких как геометрия, строительство, физика и другие. Например, зная значение диаметра, можно определить объем шара, его площадь поверхности или сравнить его размер с другими телами. Кроме того, это правило может пригодиться в повседневной жизни, например, для оценки размеров шаров и мячей, а также для выбора подходящих по размеру бильярдных шаров или мармеладных конфет.
Что такое диаметр шара и как его измерить?

Чтобы измерить диаметр шара, необходимо провести линию через его центр, соединяющую две противоположные точки на его поверхности. Эту линию можно измерить с помощью линейки или другого подходящего измерительного инструмента.
Если вы уже знаете радиус шара, то можно легко вычислить его диаметр, умножив значение радиуса на 2. Формулой для нахождения диаметра шара можно записать как:
Д = 2r
Где Д – диаметр, r – радиус.
Измерение диаметра шара имеет большое значение в геометрии, физике и других научных и инженерных областях. Зная диаметр шара, можно также вычислить его объем, площадь поверхности и другие характеристики.
Формула расчета диаметра шара по его радиусу
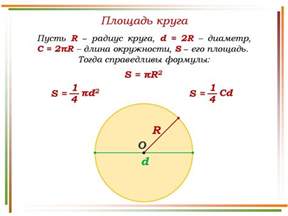
Диаметр шара (D) равен удвоенному значению его радиуса (r):
D = 2r
То есть, для расчета диаметра нужно умножить радиус на 2.
Пример расчета диаметра шара по известному радиусу
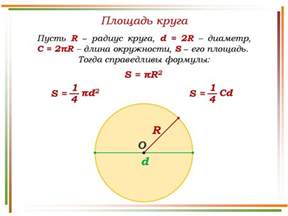
Радиус шара (r) - это расстояние от его центра до любой точки на его поверхности. Диаметр (d) - это самая длинная прямая, соединяющая две точки на поверхности шара и проходящая через его центр.
Соотношение между диаметром и радиусом шара может быть записано следующим образом:
d = 2r
Таким образом, чтобы найти диаметр шара, нужно удвоить значение его радиуса.
Например, если известно, что радиус шара равен 5 см, то диаметр можно рассчитать следующим образом:
- Умножаем значение радиуса на 2: d = 2 * 5 см
- Выполняем вычисление: d = 10 см
Таким образом, диаметр шара с радиусом 5 см составляет 10 см.
Как использовать диаметр шара в практических задачах

Вот несколько примеров, как можно использовать диаметр шара:
- Расчет объема шара: Диаметр шара используется в формуле для расчета объема шара. Объем шара можно вычислить с помощью формулы V = (4/3) * π * (r^3), где r - радиус шара. Диаметр шара полезен для расчета объема, так как его значение можно использовать для определения радиуса.
- Расчет площади поверхности шара: Диаметр шара также используется для расчета площади поверхности шара. Площадь поверхности шара можно вычислить с помощью формулы S = 4 * π * (r^2), где r - радиус шара. Диаметр может быть полезен при расчете площади поверхности.
- Расчет длины окружности: Диаметр шара также используется для расчета длины окружности. Длина окружности можно вычислить с помощью формулы L = π * d, где d - диаметр шара. Если требуется найти длину окружности, зная только диаметр, эту формулу можно применить.
- Рассмотрение механических систем: В области механики диаметр шара может использоваться для расчета силы и движения объектов. Например, при расчете силы и момента инерции вращающегося шара, диаметр может использоваться в формулах для определения этих параметров.
Узнав диаметр шара, вы можете использовать его в различных практических задачах для получения информации о размерах, объемах, площадях поверхностей и других характеристиках объектов.