Длина диагонали трапеции - один из важных параметров, который позволяет определить форму и размеры этой геометрической фигуры. Трапеция - это четырехугольник, у которого две стороны параллельны, а две другие - нет. Найти длину диагонали трапеции помогут формулы и математические выкладки. В данной статье мы расскажем вам о том, как правильно это сделать.
Первым шагом в определении длины диагонали трапеции является изучение ее основных параметров. Одна из сторон трапеции называется большей основой, а другая - меньшей. Диагонали трапеции пересекаются в точке, которая называется точкой пересечения диагоналей. В основе нахождения длины диагонали лежит связь между сторонами трапеции и ее диагоналями.
Для нахождения длины диагонали трапеции, можно использовать теорему Пифагора. Эта теорема устанавливает соотношение между квадратами длин сторон прямоугольного треугольника и квадратом длины его гипотенузы. Применяя теорему Пифагора к трапеции, можно найти длину диагонали через длины всех ее сторон и оснований. Для этого необходимо рассмотреть два прямоугольных треугольника, образованных диагоналями трапеции.
Как вычислить длину диагонали трапеции
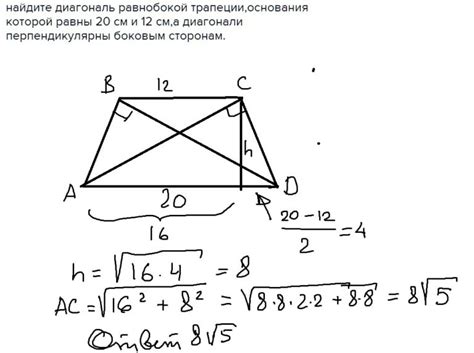
Есть несколько способов вычислить длину диагонали трапеции, в зависимости от данных, которые у вас есть. Вот некоторые из них:
1. Используя высоту и основания трапеции
Если у вас есть высота трапеции (h) и длины ее оснований (a и b), вы можете использовать теорему Пифагора для вычисления длины диагонали (d):
d = √(h² + (b-a)²)
2. Используя углы и длины сторон трапеции
Если у вас есть значения углов трапеции (α и β) и длины ее сторон (a, b, c и d), вы можете использовать закон косинусов для вычисления длины диагонали (x):
x = √(a² + b² - 2abcos(α + β))
3. Используя координаты вершин трапеции
Если у вас есть координаты вершин трапеции (A(x1, y1), B(x2, y2), C(x3, y3), D(x4, y4)), вы можете использовать формулу расстояния между двумя точками для вычисления длины диагонали:
d = √((x2 - x1)² + (y2 - y1)²)
Убедитесь, что вы выбираете подходящий метод в зависимости от данных, которыми вы располагаете. И помните, чтобы правильно измерить диагональ трапеции, вам может понадобиться линейка или другой инструмент для измерения длины.
Подготовка к вычислению длины диагонали
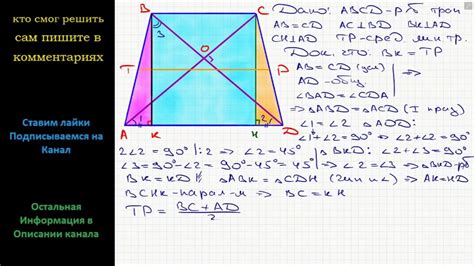
Перед началом вычисления длины диагонали трапеции необходимо собрать несколько ключевых данных:
- Запишите значения оснований трапеции. Обозначьте одно основание как "a" и другое основание как "b".
- Измерьте высоту трапеции. Обозначьте ее как "h".
- Проверьте, известно ли вам значение угла между боковой стороной и основанием "a". Если известен, обозначьте его как "α".
После сбора всех необходимых данных вы готовы приступить к вычислению длины диагонали трапеции.
Вычисление длины диагонали трапеции
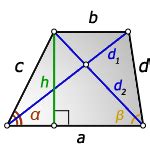
Чтобы вычислить длину диагонали, нужно выполнить следующие шаги:
- Измерьте длину основания трапеции, обозначим ее как a.
- Измерьте длину второго основания трапеции, обозначим ее как b.
- Измерьте угол между основаниями трапеции, обозначим его как ∠A.
- Преобразуйте значение угла ∠A из градусов в радианы, умножив его на (пи/180).
- Вычислите косинус угла ∠A, используя функцию cos().
- Вычислите квадрат суммы косинуса угла ∠A, умножив на сумму квадратов оснований a и b и вычтите удвоенное произведение оснований a и b на косинус угла ∠A.
- Вычислите длину диагонали, извлекая квадратный корень из полученного значения.
Примечание: Угол ∠A должен быть взят в радианах, так как функция cos() возвращает косинус угла, выраженного в радианах.
Пример вычисления длины диагонали трапеции:
Дана трапеция со значениями оснований a = 5 см и b = 7 см, а также углом ∠A = 60 градусов.
Вычислим длину диагонали:
∠A = 60 * (пи/180) = 1.047 радиан
cos(∠A) = cos(1.047) ≈ 0.5
Длина диагонали = √(a^2 + b^2 - 2abcos(∠A)) = √(5^2 + 7^2 - 2*5*7*0.5) ≈ 7.66 см