При решении геометрических задач, связанных с прямоугольным треугольником, одной из основных задач является нахождение катета по известной гипотенузе и углу. Это вопрос, который может возникнуть в школе, в университете или в повседневной жизни. На первый взгляд это может показаться сложным, но на самом деле существуют простые формулы, которые помогут вам решить эту задачу.
Пусть у нас есть прямоугольный треугольник со сторонами a, b, c, где c - гипотенуза. Известно, что угол A лежит напротив катета a. С помощью тригонометрических функций, таких как синус и косинус, мы можем найти длину катета a. Формула для нахождения катета a выглядит следующим образом:
a = c * sin(A)
Здесь c - известная длина гипотенузы, A - известный угол в радианах. С помощью этой формулы вы сможете легко найти длину катета a. Не забудьте, что при использовании тригонометрических функций угол должен быть в радианах, поэтому, если ваш угол изначально задан в градусах, необходимо преобразовать его.
Теперь у вас есть все необходимые инструменты, чтобы найти катет по известной гипотенузе и углу. Просто подставьте значения в формулу и получите результат. Надеемся, что это руководство поможет вам в решении подобных задач и облегчит вашу работу с прямоугольными треугольниками.
Что такое гипотенуза и катет?

Гипотенуза обозначается буквой "c", а катеты - буквами "a" и "b". По теореме Пифагора в прямоугольном треугольнике справедливо следующее равенство: с² = a² + b². Это равенство позволяет находить значение гипотенузы или одного из катетов при известных значениях других сторон.
Гипотенуза и катеты имеют важное значение при решении геометрических задач, особенно связанных с прямоугольными треугольниками. Например, зная длину гипотенузы и одного из катетов, можно найти длину другого катета с помощью теоремы Пифагора. Или наоборот, зная длины двух катетов, можно найти длину гипотенузы.
Важно помнить, что гипотенуза всегда является самой длинной стороной в прямоугольном треугольнике, а катеты - короче. Знание этих понятий и умение применять теорему Пифагора помогут успешно решать задачи, связанные с прямоугольными треугольниками.
Зачем нужно находить катет по гипотенузе и углу?

С помощью данной задачи можно определить размеры объектов и расстояния до них. Например, если известна длина гипотенузы и величина угла, можно рассчитать длину катета и определить расстояние до некоей точки. Это особенно полезно в случаях, когда физический доступ к объекту ограничен или невозможен.
Кроме того, нахождение катета по гипотенузе и углу помогает в решении задач, связанных с построением фигур. Зная величину угла и гипотенузу, можно определить положение вершин и сторон треугольника. Это пригодится при проектировании и строительстве сооружений, а также в других областях, где важно точно измерить и расположить элементы конструкции.
Также нахождение катета по гипотенузе и углу помогает решать различные задачи из математики и физики. Это может быть полезно при изучении геометрии, тригонометрии и других наук, где требуется анализировать информацию, связанную с треугольниками.
Короче говоря, нахождение катета по гипотенузе и углу является важным и полезным навыком, который позволяет решать разнообразные задачи и применять полученные знания на практике.
Как найти катет по гипотенузе и углу: шаг за шагом руководство
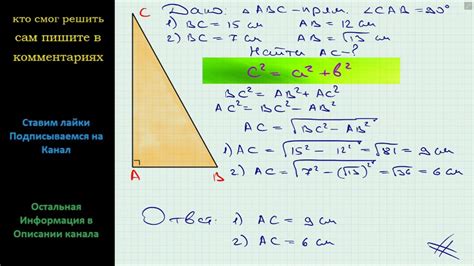
Нахождение катета прямоугольного треугольника по заданным значениям гипотенузы и угла может быть очень полезным при решении геометрических задач. Следующее руководство шаг за шагом покажет, как это сделать.
- Определите значение гипотенузы и угла треугольника.
- Используйте формулу синуса для нахождения значения противолежащего катета. Формула имеет вид sin(угол) = противолежащий катет / гипотенуза.
- Разрешите уравнение относительно противолежащего катета и выразите его в нужной форме.
- Подставьте известные значения в уравнение и вычислите значение противолежащего катета.
Пример:
- Пусть гипотенуза треугольника равна 10 и угол между гипотенузой и противолежащим катетом равен 30 градусам.
- Используя формулу sin(30°) = противолежащий катет / 10, получим sin(30°) = противолежащий катет / 10.
- Разрешим уравнение относительно противолежащего катета, умножив обе части уравнения на 10: 10 * sin(30°) = противолежащий катет.
- Подставим значение sin(30°) и вычислим противолежащий катет: 10 * 0,5 = 5. Таким образом, противолежащий катет равен 5.
Следуя этому шаг за шагом руководству, вы сможете легко и точно найти катет по гипотенузе и углу прямоугольного треугольника.
Примеры нахождения катета по гипотенузе и углу

Пример 1:
Пусть у нас есть прямоугольный треугольник ABC, в котором гипотенуза AC = 5 см, а угол BAC = 45°. Найдём катет BC.
Для начала, найдем значение синуса угла BAC. Синус угла равен отношению противолежащего катета к гипотенузе:
sin(BAC) = BC / AC
sin(45°) = BC / 5
BC = sin(45°) * 5
BC = 0.707 * 5 = 3.535 см
Пример 2:
Рассмотрим прямоугольный треугольник DEF, в котором гипотенуза DE = 10 см, а угол DFE = 30°. Найдём катет DF.
Аналогично предыдущему примеру, используем синус угла DFE:
sin(DFE) = DF / DE
sin(30°) = DF / 10
DF = sin(30°) * 10
DF = 0.5 * 10 = 5 см
Пример 3:
Пусть имеется треугольник GHI, где гипотенуза GH = 8 см, а угол GIH = 60°. Найдём катет HI.
Используем синус угла GIH:
sin(GIH) = HI / GH
sin(60°) = HI / 8
HI = sin(60°) * 8
HI = 0.866 * 8 = 6.928 см
Приведенные примеры иллюстрируют основные шаги для нахождения катета по гипотенузе и углу в прямоугольном треугольнике. Важно помнить, что для таких вычислений необходимо знать значения синуса или косинуса соответствующего угла, а также значение гипотенузы. Эта информация позволяет определить значение катета с помощью соответствующей тригонометрической формулы.
Практическое применение нахождения катета по гипотенузе и углу

- Архитектура и строительство: при проектировании и строительстве зданий и сооружений важно иметь возможность определить длину катета по известной гипотенузе и углу. Это помогает в расчете размеров и конструкций, а также в создании устойчивых и безопасных построек.
- Топографические и геодезические работы: для определения расстояний, высот и уклонов необходимо уметь применять теорему Пифагора и находить катеты треугольника по гипотенузе и известному углу. Это используется при создании карт, планов местности и измерении различных параметров земной поверхности.
- Работа с электроникой: в различных электронных устройствах, таких как компьютеры, мобильные телефоны и телевизоры, применяются печатные платы. Для расчета и размещения компонентов на печатной плате необходимо знать размеры, положение и углы треугольников, образующих эти компоненты.
- Механика и инженерия: в процессе проектирования и создания машин, автомобилей, самолетов и других механических устройств необходимо иметь возможность определить размеры и углы треугольников, которые играют важную роль в конструкции и функционировании данных устройств.
- Спорт и физические тренировки: во многих видах спорта, таких как гребля, плавание, гимнастика и т.д., важно иметь хорошую координацию и уметь выполнять определенные движения. Знание тригонометрии позволяет атлетам лучше понимать и контролировать свое движение, особенно в случае, когда требуется задать определенный угол или длину стороны движения.
Это лишь несколько примеров на практическое применение знаний о нахождении катета по гипотенузе и углу. Понимание этих концепций расширяет возможности и умения в различных областях деятельности, поэтому важно освоить их и применять в решении задач.