Длина окружности - это один из фундаментальных параметров геометрических объектов, который имеет большое значение при решении различных математических и физических задач. В данной статье мы рассмотрим, как можно вычислить длину окружности, используя радиус и число пи.
Перед тем, как перейти к расчетам, давайте разберемся, что же такое радиус и число пи. Радиус - это отрезок, проведенный от центра окружности до ее любой точки. Он является одним из основных параметров окружности и обозначается символом R.
Число пи - это математическая константа, которая обозначается греческой буквой π. Значение числа пи приближенно равно 3,14159 и представляет собой отношение длины окружности к ее диаметру. Число пи является иррациональным, что означает, что его десятичная запись не имеет повторяющихся или закономерных цифр.
Теперь, зная значения радиуса и числа пи, мы можем легко вычислить длину окружности по формуле: Длина окружности = 2 * π * R. Здесь, π умножается на радиус и на 2, чтобы получить полную длину окружности.
Определение длины окружности

Формула для определения длины окружности:
| Длина окружности | = | 2 | π | Радиус |
| = | 2 | π | r |
Где:
- π (пи) – математическая константа, примерное значение равно 3.14 или 3.14159;
- r - радиус круга.
Данная формула позволяет легко и быстро определить длину окружности только зная радиус круга. Расчет может быть выполнен вручную или с помощью калькулятора.
Формула для вычисления длины окружности
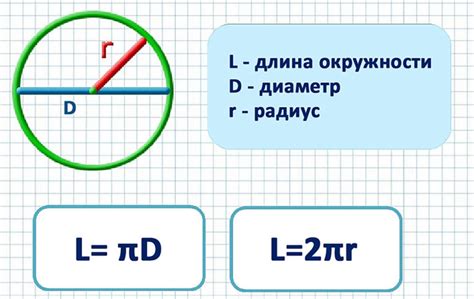
Формула для вычисления длины окружности задается следующим образом:
- Длина окружности (C) = 2 * π * радиус (r).
Для того чтобы рассчитать длину окружности, необходимо знать значение радиуса, который представляет собой расстояние от центра окружности до ее края.
Число π (пи) является математической константой, которая представляет отношение длины окружности к ее диаметру и приближенно равна 3,14159. Оно является бесконечной десятичной дробью и используется во многих математических расчетах связанных с окружностями.
Используя данную формулу, вы можете вычислить длину окружности для любого заданного значения радиуса и числа π (пи).
Значение числа пи

Число пи является иррациональным числом, что означает, что его десятичное представление не может быть точно выражено в виде обыкновенной дроби. Также число пи является трансцендентным числом, что означает, что оно не является решением уравнения с алгебраическими коэффициентами.
Значение числа пи широко используется в математике, физике, инженерии и других науках для решения различных задач, связанных с геометрией и тригонометрией. Оно также встречается в различных формулах и уравнениях, таких как формула для вычисления площади круга или формула для вычисления длины окружности.
Практическое применение формулы

Формула для вычисления длины окружности через радиус и число π имеет широкое практическое применение в различных областях науки и техники. Вот некоторые из них:
| Инженерия и архитектура | В инженерных и архитектурных расчетах длина окружности часто используется для определения длины линейных элементов, таких как трубопроводы, кабели, шпильки и т. д. При знании радиуса можно легко вычислить длину нужного элемента и подобрать подходящую длину материала. |
| Геометрия и математика | Формула длины окружности активно применяется в геометрии и математике. Она является одним из базовых понятий геометрии и используется при решении различных задач, таких как вычисления площади круга, определение дуги окружности и нахождение периметра сложных фигур. |
| Физика и наука о материалах | В физике и науке о материалах длина окружности может быть необходима для определения пути, пройденного материалом, например, волокнами или проводниками при их вращении. Это может быть полезно при проектировании электрических установок или работы с материалами в промышленности. |
| Картография и навигация | В картографии и навигации длина окружности может быть использована для измерения расстояний на земле или на море. Например, при планировании маршрута судна или вычислении периметра острова, знание длины окружности может быть весьма полезным. |
И это только некоторые из множества примеров применения формулы для вычисления длины окружности. Эта формула является важным инструментом в различных научных и практических областях, где величины, связанные с окружностями, играют роль.
Важность точного вычисления длины окружности
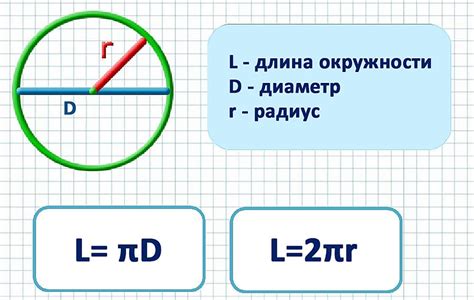
При точном вычислении длины окружности, основой служит значение числа π. Это иррациональное число, которое примерно равно 3,14159. Оно используется для определения отношения длины окружности к ее диаметру. Благодаря этому соотношению мы можем вычислить длину окружности, зная только ее радиус.
Точность вычислений играет важную роль в следующих сферах:
1. Геометрия: Вычисление длины окружности является одним из основных заданий в геометрии. Оно позволяет определить периметр окружности и использовать эту информацию в различных геометрических конструкциях и формулах.
2. Физика: Длина окружности также играет важную роль в физике. Она задает путь, который проходит точка при движении по окружности. Это позволяет нам определить скорость, ускорение и другие физические параметры объектов, движущихся по окружности.
3. Инженерные расчеты: В инженерных отраслях, таких как строительство, машиностроение и электротехника, точное вычисление длины окружности имеет огромное значение. Оно помогает определить необходимую длину кабеля, трубы или других конструктивных элементов, что является важным условием безопасной и эффективной реализации проектов.
Точное вычисление длины окружности через радиус и число π является основой для многих приложений и применений. Понимание важности точности в этих вычислениях позволяет нам правильно расчеты и перенести их результаты в жизнь, обеспечивая надежность и эффективность различных процессов и проектов.