Цилиндр - это геометрическое тело, состоящее из двух равных и параллельных кругов, или окружностей, и боковой поверхности, которая соединяет эти окружности. Для решения различных задач, связанных с цилиндром, необходимо знать его основные характеристики, включая длину окружности основания.
Для определения длины окружности основания цилиндра необходимо знать значение радиуса окружности. Радиус - это расстояние от центра окружности до любой ее точки. Используется следующая формула для расчета длины окружности:
C = 2 * π * r
Где С - длина окружности, r - радиус окружности, а π (пи) - математическая константа, примерное значение которой равно 3,14159.
Для вычисления длины окружности основания цилиндра необходимо умножить значение радиуса на два и на число π. Полученный результат будет представлять собой значение длины окружности в выбранной системе измерения (например, в сантиметрах, метрах и т. д.).
Как найти длину окружности
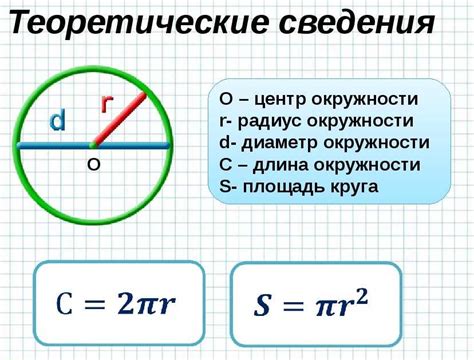
Формула для расчета длины окружности основывается на радиусе окружности - расстоянии от центра окружности до любой точки на ее окружности. Формула имеет вид:
Длина окружности = 2 * π * радиус
где π равно примерно 3.14159. Данное число является математической константой пи и используется в геометрических расчетах.
1. Взять значение радиуса окружности.
2. Умножить значение радиуса на 2π.
3. Получить результат, который является длиной окружности.
Длина окружности очень полезна при решении задач по геометрии, строительству, физике и другим наукам. Знание формулы и умение применять ее в решении задач помогут вам легко находить данную величину и применять ее в нужных ситуациях.
Определение окружности

Для определения окружности необходимо знать радиус, который представляет собой расстояние от центра окружности до любой ее точки. Радиус обозначается символом "r".
Окружность может быть полная или неполная. Полная окружность образуется, когда ее длина окружности равна удвоенной площади окружности.
Длина окружности может быть определена по формуле:
| Формула: | Длина окружности (C) = 2πr |
В этой формуле "π" (пи) – это число, которое примерно равно 3.14159 или можно использовать приближенное значение 3.14.
Таким образом, для определения длины окружности основания цилиндра необходимо знать радиус основания (r) и применить формулу длины окружности.
Значение длины окружности
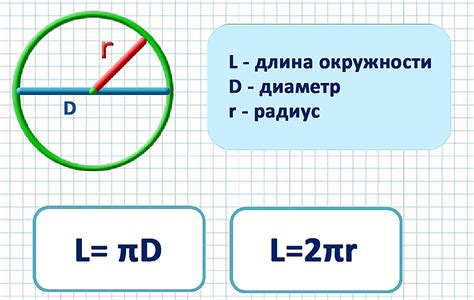
Формула для расчета длины окружности основания цилиндра:
C = πd = 2πr
Здесь:
- C - длина окружности;
- d - диаметр окружности;
- r - радиус окружности;
- π - математическая константа, примерное значение которой равно 3.14159 (или приближенно 22/7).
Используя данную формулу, вы можете легко найти длину окружности основания цилиндра, поскольку радиус или диаметр обычно указаны в условиях задачи или можно измерить с помощью инструментов.
Знание значения длины окружности основания цилиндра позволит вам решать различные задачи в геометрии, строительстве, технике и других областях, где цилиндры играют важную роль.
Основания цилиндра
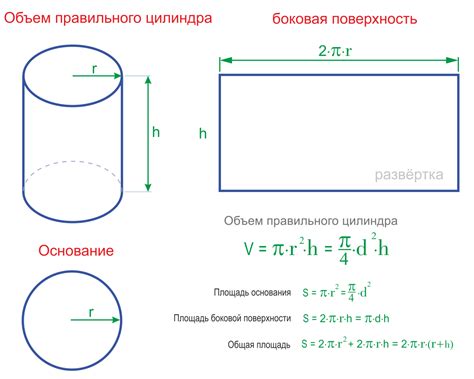
Для расчета длины окружности основания цилиндра используется следующая формула:
| Длина окружности (C) | = | 2 * π * r |
Где:
- C - длина окружности основания цилиндра
- π - математическая константа, приближенное значение которой равно 3.14159
- r - радиус окружности основания цилиндра
Таким образом, чтобы найти длину окружности основания цилиндра, необходимо умножить радиус на два и на значение π.
Зная длину окружности основания, можно решать различные задачи, связанные с объемом и площадью поверхности цилиндра.
Понятие основания цилиндра
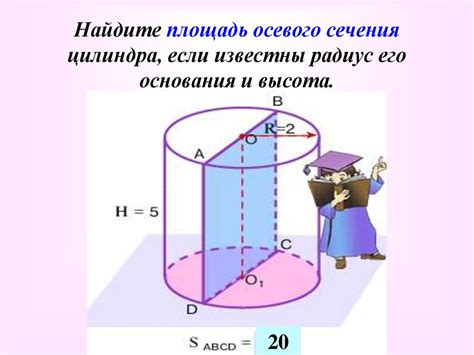
Если основаниями цилиндра являются параллелограммы, то такой цилиндр называется пластинчатым. Параллелограммы могут быть прямоугольными или ромбическими, что влияет на форму самого цилиндра.
Если основаниями цилиндра являются круги, то такие цилиндры называются круговыми. Они являются самыми распространенными типами цилиндров и встречаются в повседневной жизни, например, в виде банок, стеклянных банок и т. д.
Основания цилиндра играют важную роль при определении его свойств и параметров, таких как площадь поверхности и объем. Знание понятия основания цилиндра необходимо для осуществления различных геометрических расчетов и удобного представления данной фигуры.
 |  |
| Цилиндр с круговым основанием | Цилиндр с пластинчатым основанием |
Использование формул
Для расчета длины окружности основания цилиндра необходимо использовать соответствующую формулу. Формула для расчета длины окружности имеет вид:
| Длина окружности основания цилиндра (L) | = | 2 × π × r |
где:
- L - длина окружности основания цилиндра;
- π - число Пи, приближенное значение которого составляет примерно 3.14159;
- r - радиус окружности основания цилиндра.
Для использования данной формулы необходимо знать значение радиуса окружности основания цилиндра. Радиус можно определить с помощью других формул, например, используя известные значения диаметра цилиндра или площади основания.
После определения значения радиуса можно подставить его в формулу для расчета длины окружности основания цилиндра и выполнить необходимые математические операции, чтобы получить итоговое значение длины окружности.
Таким образом, зная радиус окружности основания цилиндра, вы можете использовать соответствующую формулу для точного расчета длины окружности. Это поможет вам не только в практических задачах, связанных с цилиндрами, но и в области геометрии и математики в целом.
Как измерить длину окружности основания

Измерение длины окружности основания цилиндра может показаться сложной задачей, но на самом деле это достаточно просто.
Для измерения длины окружности основания вам понадобится измерительная лента или линейка. Начните измерение с любой точки окружности и протяните ленту или линейку вокруг окружности, закрепив ее на месте.
Убедитесь, что лента или линейка плотно прилегает к окружности и не смещается. Затем прочитайте измеренное значение длины окружности, которое будет выражено в выбранной единице измерения, например в сантиметрах или дюймах.
Если вы хотите найти длину окружности основания цилиндра с использованием математической формулы, для этого можно использовать формулу:
C = 2πr, где C - длина окружности, π - число пи (приблизительно равное 3,14159) и r - радиус окружности, которую можно найти с помощью других известных размеров цилиндра.
Убедитесь, что радиус указан в той же единице измерения, что и результат, который вы хотите получить. Если радиус указан, например, в сантиметрах, результат будет выражен в сантиметрах.
Теперь, когда вы знаете, как измерить длину окружности основания, вы можете использовать эту информацию для решения различных задач, связанных с цилиндром, например, для определения объема цилиндра или для расчета площади поверхности.