Правильный шестиугольник – это многоугольник с шестью равными сторонами и углами. Эта геометрическая фигура имеет множество применений в архитектуре, науке и искусстве. Одним из важных параметров правильного шестиугольника является его окружность – замкнутая кривая, состоящая из всех точек, равноудаленных от центра шестиугольника.
Однако иногда нам может понадобиться узнать длину этой окружности, основываясь только на площади правильного шестиугольника. На первый взгляд, это может показаться сложной задачей, но на самом деле существует простая формула, позволяющая найти длину окружности по площади шестиугольника.
Для этого нам потребуется использовать знания математики и геометрии. Основной инструмент, с помощью которого мы решим эту задачу, – формула для нахождения радиуса окружности по площади шестиугольника. Следуя несложным шагам, мы сможем найти длину окружности, используя эту формулу и простые математические операции.
Формула для расчета площади правильного шестиугольника

Пусть a - длина стороны правильного шестиугольника. Тогда его площадь S может быть вычислена по формуле:
S = 3√3 * a^2 / 2
где √3 - корень из числа 3, а ^2 - обозначение для возведения в квадрат. Таким образом, для нахождения площади правильного шестиугольника нужно умножить квадрат длины его стороны на 3√3, а затем разделить полученный результат на 2.
Используя данную формулу, можно эффективно вычислить площадь правильного шестиугольника и использовать полученный результат для дальнейших расчетов или анализа.
Нахождение радиуса описанной окружности вокруг шестиугольника
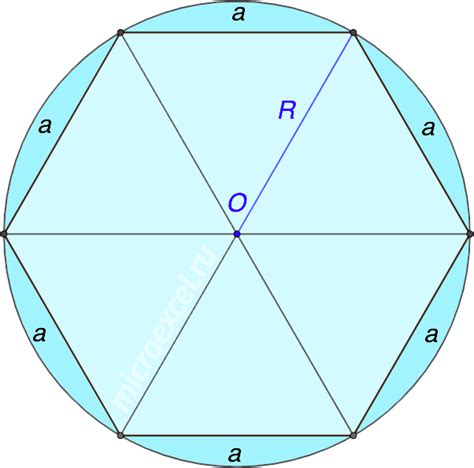
Радиус описанной окружности вокруг правильного шестиугольника можно найти с помощью формулы, основанной на площади исходного многоугольника:
Рассмотрим правильный шестиугольник со стороной a. Пусть R - радиус описанной окружности вокруг него.
Площадь такого шестиугольника можно найти с помощью формулы:
S = (3√3 * a^2) / 2,
где S - площадь шестиугольника, a - длина стороны.
Радиус описанной окружности R связан с площадью шестиугольника S следующим образом:
R = a / (2√3),
где R - радиус описанной окружности.
Таким образом, имея площадь шестиугольника S, можно найти радиус описанной окружности R.
Нахождение радиуса вписанной окружности в шестиугольник
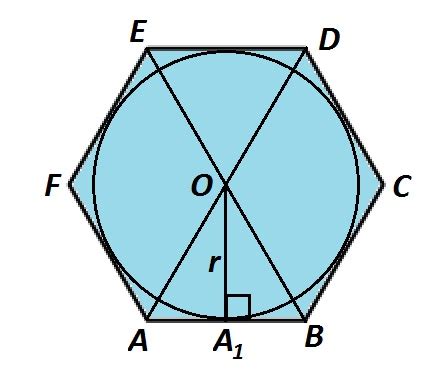
Для начала, найдем длину стороны правильного шестиугольника по его площади. Формула для нахождения длины стороны имеет вид:
s = √(4A/√3)
где s - длина стороны шестиугольника, A - площадь шестиугольника, √ - знак квадратного корня, √3 - квадратный корень из трех.
Зная длину стороны s, радиус вписанной окружности может быть найден по следующей формуле:
r = s/(2√3)
где r - радиус вписанной окружности.
Таким образом, применяя эти формулы, можно найти радиус вписанной окружности в правильный шестиугольник по известной площади этой фигуры.
Расчет длины окружности по радиусу
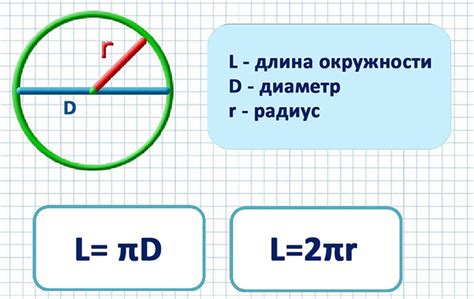
Формула для расчета длины окружности:
- C = 2πr
Где:
- C - длина окружности,
- π (пи) - математическая константа, приближенное значение которой равно 3,14159,
- r - радиус окружности.
Таким образом, чтобы найти длину окружности, нужно умножить радиус окружности на 2π. Например, если радиус окружности равен 5 сантиметрам, то длина окружности будет:
- C = 2 * 3,14159 * 5 = 31,4159 сантиметров.
Теперь вы знаете, как рассчитать длину окружности по радиусу!
Применение формулы для правильного шестиугольника

Для нахождения длины окружности правильного шестиугольника по его площади существует определенная формула.
Рассчитать длину окружности можно, зная площадь шестиугольника по формуле:
S = 3 × a × H,
где S - площадь шестиугольника, a - длина его стороны, а H - высота.
Сначала нужно найти длину стороны, исходя из площади шестиугольника. Для этого применяется формула:
a = √(S / (3 × √3)).
Затем можно вычислить высоту шестиугольника с помощью формулы:
H = a × √3 / 2.
Теперь, имея все необходимые значения, можно подставить их в формулу для нахождения длины окружности:
Окружность = 2 × π × R,
где R - радиус окружности.
Таким образом, зная площадь правильного шестиугольника, можно вычислить длину его окружности, применяя соответствующие формулы.
Обратите внимание, что в данном контексте предполагается, что шестиугольник является правильным (имеет равные стороны и углы) и что он вписан в окружность.
Пример расчета длины окружности правильного шестиугольника
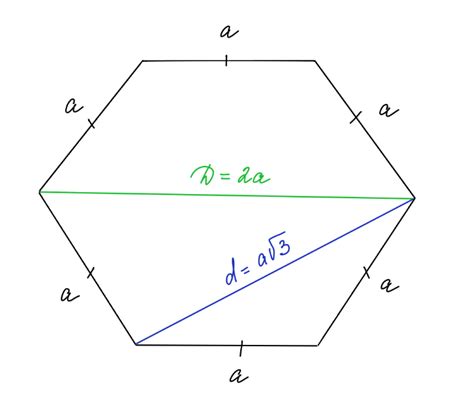
Для расчета длины окружности правильного шестиугольника необходимо знать его площадь. Предположим, что площадь шестиугольника равна S единицам площади.
Сначала найдем длину стороны шестиугольника. Для этого воспользуемся формулой:
a = √(s / (3√3/2)),
где a - длина стороны шестиугольника.
После нахождения длины стороны шестиугольника, длина окружности может быть найдена по формуле:
C = 6a,
где C - длина окружности шестиугольника.
Таким образом, по известной площади шестиугольника мы можем рассчитать его длину окружности с помощью формулы.