Прямоугольные треугольники – это одна из самых базовых и важных фигур в геометрии. Они встречаются во многих различных задачах и областях науки, начиная от физики и астрономии и заканчивая строительством и дизайном. Понимание, как найти сторону прямоугольного треугольника, является основой для решения многих задач.
В этой статье мы рассмотрим формулы, основанные на теореме Пифагора и тригонометрии, которые помогут нам найти неизвестные стороны прямоугольного треугольника.
Первая и, пожалуй, самая известная формула, называется теоремой Пифагора. Она гласит, что сумма квадратов катетов равна квадрату гипотенузы. Если у нас есть известные значения двух сторон прямоугольного треугольника, то мы можем использовать эту формулу для нахождения третьей стороны. Например, если длина одного из катетов равна 3, а гипотенузы – 5, мы можем найти второй катет путем вычитания квадрата первого катета из квадрата гипотенузы.
Однако, иногда у нас нет известных значений сторон прямоугольного треугольника, и мы должны найти их, используя формулы тригонометрии. Для этого нам понадобятся три известные величины: угол, противолежащий искомой стороне, угол, примыкающий к искомой стороне, и гипотенуза.
Определение прямоугольного треугольника

Прямоугольный треугольник имеет особые свойства и отношения между его сторонами и углами. Одна из наиболее известных формул, которая позволяет найти стороны треугольника, называется теоремой Пифагора:
a² + b² = c²
В этой формуле, a и b являются катетами треугольника, а c – гипотенузой. Гипотенуза представляет собой сторону треугольника, противоположную прямому углу.
Если известны значения двух сторон треугольника, можно использовать тригонометрические функции – синус, косинус и тангенс – для определения значений углов треугольника и оставшейся стороны.
Используя эти формулы и соотношения, можно решать разнообразные задачи, связанные с прямоугольными треугольниками. Знание и понимание особенностей этих треугольников расширяет возможности в сфере геометрии и тригонометрии, и может быть полезно в различных областях науки, техники и практических применений.
Формула синуса
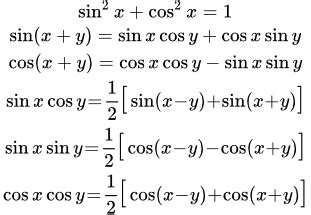
Формула синуса выглядит следующим образом:
sin(α) = a / c |
Где:
- sin(α) - синус угла α;
- a - противолежащая катета;
- c - гипотенуза.
Из данной формулы можно выразить противолежащую катету:
a = sin(α) * c |
Таким образом, если известны синус угла и значение гипотенузы, можно вычислить длину противолежащей катеты.
Эта формула особенно полезна, когда известны угол и гипотенуза, но неизвестна длина противолежащей катеты.
Формула синуса - важный инструмент в геометрии и находит применение не только в вычислении сторон прямоугольного треугольника, но и в других областях, включая физику, астрономию и инженерию.
Формула косинуса
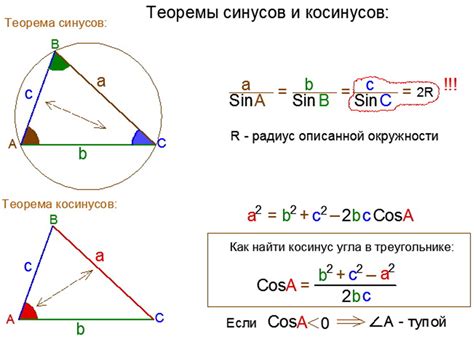
Формула косинуса имеет следующий вид:
a = √(b² + c² - 2bc * cos(A))
где:
- a - искомая сторона треугольника;
- b и c - длины известных сторон треугольника;
- A - величина угла между известными сторонами треугольника.
Формула позволяет найти сторону треугольника, если известны все ее стороны и один из углов, что делает ее одним из наиболее универсальных способов решения задач связанных с прямоугольными треугольниками.
Формула тангенса
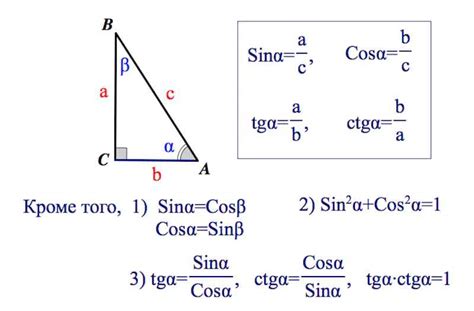
Тангенс угла в прямоугольном треугольнике можно вычислить по формуле:
тан(A) = a/b
где тан(A) - тангенс угла A, a - противолежащая сторона к углу A, b - прилежащая сторона к углу A.
Зная значения противолежащей и прилежащей стороны, можно вычислить тангенс угла, который даст нам необходимую информацию о стороне треугольника.
Применяя формулу тангенса, можно рассчитать длину стороны треугольника, если известны значения других сторон.
Например, пусть у нас есть прямоугольный треугольник, в котором известны значение противолежащей стороны a и угла A. Мы также знаем значение прилежащей стороны b. Используя формулу тангенса, мы можем рассчитать значение неизвестной стороны по формуле:
a = b * тан(A)
Таким образом, формула тангенса позволяет нам находить стороны прямоугольного треугольника, используя значения других сторон и углов.