Треугольник – это одна из самых простых и изучаемых фигур в геометрии. Он обладает тремя сторонами и тремя углами, каждый из которых можно измерить и посчитать. Однако иногда возникают ситуации, когда известны только значения углов, а нужно найти длины сторон треугольника. Для решения таких задач можно использовать косинус-формулу.
Косинус-формула позволяет найти длину одной стороны треугольника, если известны длины двух других сторон и угол между ними. Формула основана на законе косинусов, который устанавливает взаимосвязь между сторонами и углами треугольника. Косинус угла определяется отношением длин катета и гипотенузы в прямоугольном треугольнике.
Применение косинус-формулы позволяет находить неизвестные стороны треугольника и решать различные задачи, связанные с измерением и углами и сторон. Кроме того, данная формула является основой для построение графиков и диаграмм в различных областях науки и техники.
Определение косинус-формулы треугольника
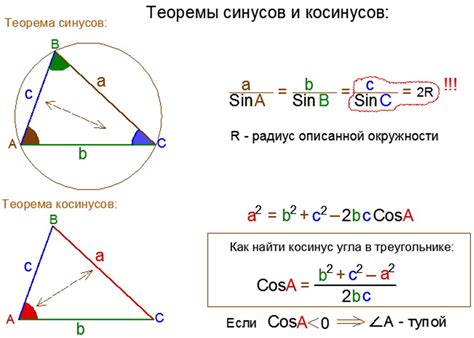
Косинус-формула выражает отношение стороны треугольника к косинусу противолежащего ей угла. Формула состоит из уравнений, позволяющих найти одну из сторон, если известны длины двух других сторон и угол между ними.
Для применения косинус-формулы треугольника необходимо знать длины двух сторон и угол между ними. Предположим, что известны стороны (a) и (b) треугольника, а также угол между этими сторонами (с). Используя косинус угла, косинус-формула треугольника может быть записана следующим образом:
| a2 = b2 + c2 - 2bccos(α) |
| b2 = a2 + c2 - 2accos(β) |
| c2 = a2 + b2 - 2abcos(γ) |
Где (α), (β) и (γ) - углы треугольника, а a, b и c - соответствующие стороны.
Косинус-формула треугольника позволяет определить отсутствующую сторону треугольника на основе известных длин двух сторон и угла между ними. Это полезный инструмент для решения геометрических задач и нахождения неизвестных значений в треугольниках.
Польза использования косинус-формулы

Одним из основных преимуществ косинус-формулы является возможность вычислить длину недостающей стороны треугольника без необходимости проводить дополнительные измерения или использовать сложные методы. Это особенно полезно в ситуациях, когда невозможно измерить сторону напрямую, например, при работе с картографическими данными или в астрономии.
Косинус-формула также находит применение при решении задач, связанных с определением площади треугольника. Зная длины всех сторон и углов треугольника, можно использовать косинус-формулу для вычисления площади без необходимости разбивать треугольник на более простые фигуры и проводить сложные расчеты.
Благодаря своей простоте и широкому спектру применения, косинус-формула является неотъемлемым инструментом для решения различных задач в геометрии, физике, строительстве и других областях науки и техники. Говоря кратко, использование косинус-формулы значительно упрощает и ускоряет процесс решения задач, связанных с треугольниками.
Пример использования косинус-формулы

Рассмотрим следующий пример. У нас есть треугольник ABC, где сторонами являются AB, BC и AC, а углами - углы А, В и С. Необходимо найти длину стороны AB.
1. Запишем косинус-формулу для стороны AB:
| AB^2 | = | AC^2 + BC^2 - 2 * AC * BC * cos(A) |
2. Подставим известные значения в формулу. Пусть AC = 5, BC = 8, A = 60°:
| AB^2 | = | 5^2 + 8^2 - 2 * 5 * 8 * cos(60°) |
3. Вычислим значение косинуса 60°, которое равно 0.5:
| AB^2 | = | 25 + 64 - 2 * 5 * 8 * 0.5 |
4. Упростим выражение:
| AB^2 | = | 25 + 64 - 40 |
5. Выполним вычисления:
| AB^2 | = | 49 |
6. Извлекаем квадратный корень, чтобы найти значение стороны AB:
| AB | = | √49 |
7. Получаем итоговый результат:
| AB | = | 7 |
Таким образом, длина стороны AB треугольника ABC равна 7.
Как найти сторону треугольника с использованием косинус-формулы

Для использования косинус-формулы необходимо знать значения длин сторон треугольника и значение угла между этими сторонами. После этого можно применить формулу:
c2 = a2 + b2 - 2ab * cos(C)
где c - искомая сторона, a и b - известные стороны треугольника, С - угол между этими сторонами.
Для нахождения искомой стороны треугольника нужно:
- Знать значения длин двух известных сторон треугольника.
- Знать значение угла между этими сторонами.
- Подставить известные значения в косинус-формулу и выполнить вычисления.
Полученное значение будет являться длиной искомой стороны треугольника.
Косинус-формула позволяет находить стороны треугольника, если известны значения двух других сторон и угол между ними. Используя эту формулу, можно решать различные задачи, например, определять геометрические свойства треугольника или находить длины его сторон при известных углах.
Применение косинус-формулы в геометрии:
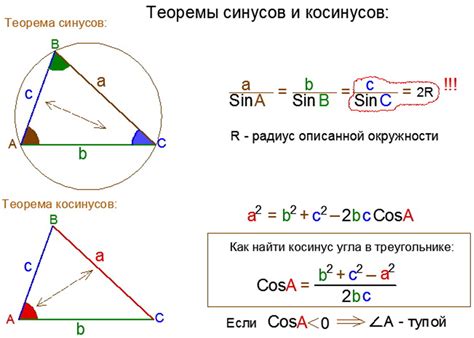
Если в треугольнике ABC известны длины сторон AB и AC, а также угол BAC (α), то можно использовать косинус-формулу для нахождения длины стороны BC:
BC = √(AB^2 + AC^2 - 2 * AB * AC * cos(α))
Косинус-формула основана на геометрической теореме, утверждающей, что квадрат длины стороны треугольника равен сумме квадратов длин остальных двух сторон, уменьшенной на удвоенное произведение этих сторон на косинус угла между ними.
При использовании косинус-формулы важно обратить внимание на то, что углы должны быть выражены в радианах, а стороны измерены в одних и тех же единицах длины.
Применение косинус-формулы в геометрии позволяет решать разнообразные задачи, включая определение длины третьей стороны треугольника по известным углам и сторонам, а также нахождение неизвестных углов по известным сторонам.
Можно считать косинус-формулу одним из базовых инструментов геометрии, который помогает строить и анализировать различные фигуры, в том числе треугольники, и решать разнообразные задачи с их участием.
Как найти угол треугольника с использованием косинус-формулы
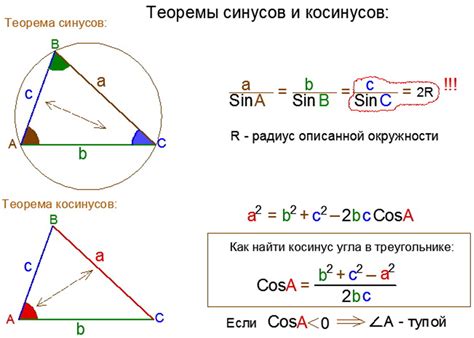
Для использования косинус-формулы необходимо иметь информацию о длинах двух сторон треугольника и угле между ними. Формула выглядит следующим образом:
cos(A) = (b^2 + c^2 - a^2) / (2bc)
где cos(A) - косинус угла A, a, b, c - стороны треугольника, противолежащие углам A, B, C соответственно.
Для нахождения угла треугольника необходимо выполнить следующие шаги:
- Запишите известные значения сторон треугольника и угол, для которого требуется найти значение;
- Подставьте значения в косинус-формулу;
- Решите уравнение и найдите значение косинуса угла;
- Используйте обратную функцию косинуса (арккосинус), чтобы найти значение угла.
Например, пусть у нас есть треугольник ABC, где известны стороны a = 7, b = 9 и угол C = 60 градусов. Чтобы найти угол A, мы будем использовать косинус-формулу следующим образом:
cos(A) = (b^2 + c^2 - a^2) / (2bc)
cos(A) = (9^2 + 7^2 - 9^2) / (2 * 9 * 7)
cos(A) = (81 + 49 - 81) / (126)
cos(A) = 49 / 126
Теперь, чтобы найти значение угла A, мы должны применить арккосинус косинуса A:
A = arccos(49 / 126)
Используя калькулятор или математическое программное обеспечение, мы найдем, что значение угла A равно примерно 66.14 градусов.
Таким образом, с использованием косинус-формулы вы сможете находить неизвестные углы треугольника, если у вас есть достаточно информации о сторонах и других углах.