Треугольник является одной из основных геометрических фигур, и его длина – важный параметр, которым часто интересуются при решении различных задач. Определить длину треугольника можно с помощью различных методов и формул. Одним из наиболее простых способов расчета является использование теоремы Пифагора.
Теорема Пифагора устанавливает, что в прямоугольном треугольнике сумма квадратов двух катетов равна квадрату гипотенузы. В этой формуле стороны треугольника обозначаются как a, b и c, где a и b – катеты, а c – гипотенуза. Таким образом, для определения длины треугольника необходимо знать длины двух его сторон – катетов, и по формуле Пифагора можно вычислить значение гипотенузы.
Применение теоремы Пифагора к треугольникам с неизвестными сторонами помогает решать задачи разной сложности. Например, если известны длины двух сторон, можно применить теорему Пифагора для нахождения длины третьей стороны. Если известны длины всех трех сторон, можно проверить, является ли треугольник прямоугольным. В данном случае длина гипотенузы будет равна корню из суммы квадратов длин двух других сторон
Найти длину треугольника

Периметр треугольника равен сумме длин его сторон. Если известны длины всех трех сторон, то периметр можно найти путем сложения этих длин. Это наиболее простой случай.
Однако часто бывает, что известны не все стороны треугольника. В таких случаях можно использовать теорему Пифагора для нахождения недостающей стороны.
Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Если известны длины двух сторон треугольника и одна из них является гипотенузой, можно найти длину недостающего катета путем применения теоремы Пифагора.
Если известны длины двух сторон треугольника и угол между ними, можно использовать закон косинусов для нахождения длины третьей стороны. Формула для расчета длины стороны A в пространстве с координатами (x1, y1) и (x2, y2) выглядит следующим образом:
|A| = sqrt((x2 - x1)^2 + (y2 - y1)^2)
Таким образом, в зависимости от известных данных, можно использовать различные способы для нахождения длины треугольника. Выбор метода зависит от конкретной ситуации.
Простой способ расчета длины треугольника
Для расчета длины треугольника нам потребуются три стороны треугольника. Обозначим их как a, b и c.
Прежде чем начать расчет, необходимо проверить, является ли треугольник правильным. Если треугольник является правильным, то сумма длин двух его сторон должна быть больше третьей стороны. Если это условие не выполняется, то треугольник неправильный и его длину невозможно рассчитать.
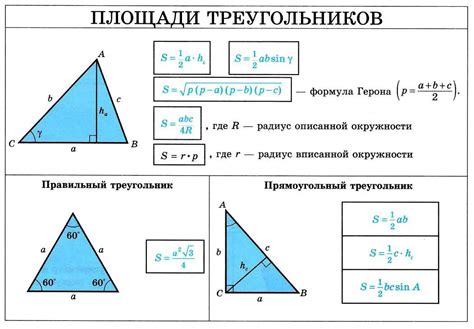
Определение длины треугольника производится по формуле Герона:
- Вычисляем полупериметр треугольника по формуле p = (a + b + c) / 2.
- Подставляем полученное значение полупериметра в формулу Герона: S = √(p * (p - a) * (p - b) * (p - c)), где S - площадь треугольника.
- Длина треугольника равна длине одной из его сторон. Выбираем ту сторону, длину которой нам необходимо определить.
Таким образом, мы можем рассчитать длину треугольника простым способом, используя формулу Герона и значения его сторон. Знание этого метода позволит нам легко определить длину треугольника в любой ситуации.
Формула для вычисления длины треугольника
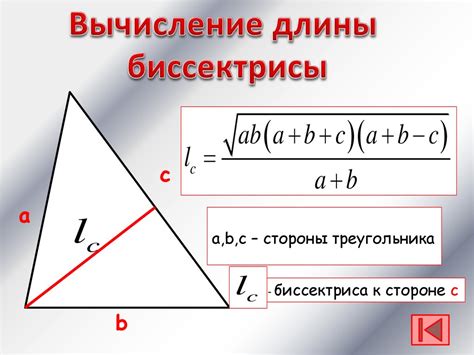
Три стороны треугольника, которые соединяют его вершины, определяют его длину.
Общий метод для вычисления длины треугольника, известный как теорема Пифагора, может быть применен в случае, когда известны длины двух сторон треугольника.
В этом случае длина третьей стороны может быть найдена с использованием следующей формулы:
c = √(a² + b²)
где:
- a - длина первой стороны треугольника,
- b - длина второй стороны треугольника,
- c - длина третьей стороны треугольника.
Формула Пифагора основана на известной теореме, которая утверждает, что сумма квадратов длин катетов равна квадрату гипотенузы в прямоугольном треугольнике.
Применяя эту формулу к произвольному треугольнику, мы можем узнать его длину, даже если у нас нет прямого угла.
Это особенно полезно при решении задач, связанных с планированием и измерением физических объектов, где точность измерений необходима для достижения нужных результатов.
Расчет длины треугольника на основе его сторон
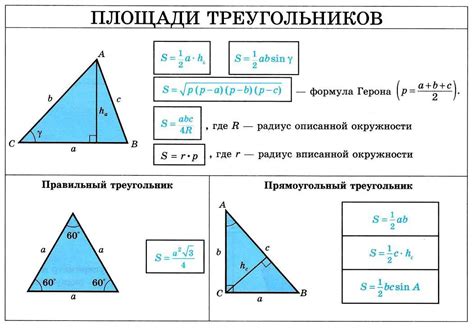
Периметр треугольника равен сумме длин его сторон. А значит, чтобы найти длину треугольника, нам достаточно сложить длины всех его сторон. Пусть стороны треугольника обозначены как a, b и c. Тогда длина треугольника L будет равна сумме этих сторон:
L = a + b + c
Например, если длины сторон треугольника равны 5, 7 и 9, то его длина будет:
L = 5 + 7 + 9 = 21
Таким образом, длина треугольника составляет 21 единицу длины.
Этот метод расчета длины треугольника особенно полезен, когда у вас есть измерения его сторон, но нет других данных, таких как углы или высоты.
Вычисление длины треугольника по теореме Пифагора

Теорема утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов:
a2 + b2 = c2
Где:
- a и b - длины катетов треугольника
- c - длина гипотенузы треугольника
Для использования теоремы Пифагора в вычислении длины треугольника, необходимо измерить длины двух сторон треугольника, которые являются катетами.
Вычисление длины гипотенузы производится по формуле:
c = √(a2 + b2)
Таким образом, если известны длины катетов треугольника, можно легко использовать теорему Пифагора для вычисления длины гипотенузы и других сторон треугольника.
Теорема Пифагора широко используется в геометрии и физике для решения различных задач, связанных с прямоугольными треугольниками.
Основные шаги для определения длины треугольника
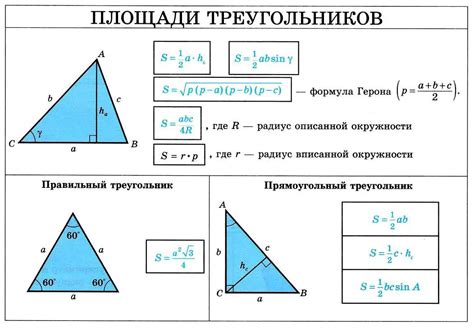
Определение длины треугольника может быть достаточно простым, если у вас есть некоторая изначальная информация. Вот несколько шагов, которые помогут вам определить длину треугольника.
- Изучите информацию о треугольнике: у вас должны быть известны хотя бы два из следующих элементов треугольника - длины сторон, углы или высоты.
- Используйте теорему Пифагора: если у вас известны длины двух сторон треугольника, вы можете найти длину третьей стороны, используя теорему Пифагора (a^2 + b^2 = c^2), где a и b - длины известных сторон, а c - длина третьей стороны.
- Примените правила синусов и косинусов: если у вас известны длины двух сторон и угол между ними, вы можете использовать правила синусов и косинусов, чтобы определить длину третьей стороны или другие углы треугольника.
- Используйте формулу полупериметра: если у вас известны длины всех трех сторон, вы можете использовать формулу полупериметра (s = (a + b + c) / 2) для определения площади треугольника.
- Примените формулу Герона: если у вас известны длины всех трех сторон, вы можете использовать формулу Герона (s * (s-a) * (s-b) * (s-c)) для определения площади треугольника, где s - полупериметр треугольника.
Следование этим основным шагам поможет вам определить длину треугольника с помощью простых расчетов. Это важные навыки для изучения геометрии и решения различных задач, связанных с треугольниками.
Как избежать ошибок при вычислении длины треугольника
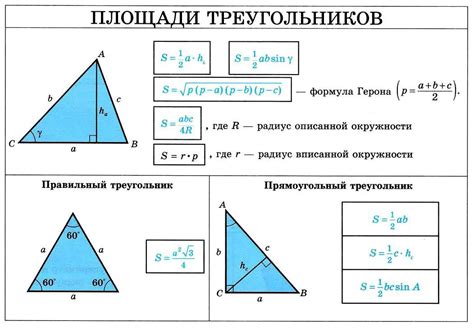
1. Правильно измерьте стороны треугольника: для получения точного результата, важно правильно измерить длины всех сторон треугольника, используя соответствующие инструменты, такие как линейка или мерная лента. Отсутствие точности в измерениях может привести к неправильному результату.
2. Используйте величины в правильных единицах измерения: проверьте, что все величины, которые вы используете в формулах для вычисления длины треугольника, измерены в одинаковых единицах. Например, если одна сторона измерена в метрах, то и остальные стороны и длина треугольника должны быть также выражены в метрах, чтобы избежать ошибок в расчетах.
3. Проверьте формулы и методы вычисления: перед применением определенных формул или методов для вычисления длины треугольника, убедитесь, что они соответствуют типу треугольника, который вы имеете. Например, для прямоугольного треугольника можно использовать теорему Пифагора, но для треугольника произвольной формы это правило может быть неприменимо. Внимательно изучите математические аспекты, связанные с вашим треугольником, и выберите подходящую формулу или метод для вычисления его длины.
4. Перепроверьте свои расчеты и результаты: после завершения вычислений длины треугольника перепроверьте свою работу и результаты, чтобы исключить возможные ошибки. Пересчитайте все значения и убедитесь, что они соответствуют друг другу и логически обоснованы. Чем более тщательно вы проверяете свою работу, тем меньше шансов на наличие ошибок.
Избегая ошибок в вычислении длины треугольника, вы сможете получить более точные результаты и улучшить свои навыки работы с геометрическими фигурами. Следуйте рекомендациям, указанным выше, и не бойтесь проверять свою работу, чтобы достичь наилучших результатов.
Примеры с расчетом длины треугольника
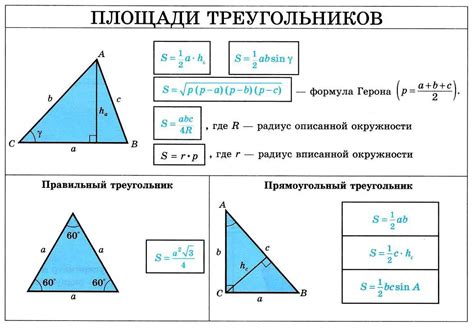
Для расчета длины треугольника необходимо знать длину каждой из его сторон. Рассмотрим несколько примеров.
Пример 1:
Известны стороны треугольника: a = 5, b = 7, c = 9. Найдем длину треугольника.
Для нахождения длины треугольника можно использовать формулу полупериметра (p). Сначала найдем полупериметр по формуле:
p = (a + b + c) / 2 = (5 + 7 + 9) / 2 = 21 / 2 = 10.5
Затем используем формулу Герона для нахождения площади треугольника:
S = sqrt(p * (p - a) * (p - b) * (p - c)) = sqrt(10.5 * (10.5 - 5) * (10.5 - 7) * (10.5 - 9)) = sqrt(10.5 * 5.5 * 3.5 * 1.5) = sqrt(623.4375) ≈ 24.96
Таким образом, длина треугольника составляет примерно 24.96 единицы длины.
Пример 2:
Известны стороны треугольника: a = 3, b = 4, c = 5. Найдем длину треугольника.
Применим ту же последовательность действий:
p = (a + b + c) / 2 = (3 + 4 + 5) / 2 = 12 / 2 = 6
S = sqrt(p * (p - a) * (p - b) * (p - c)) = sqrt(6 * (6 - 3) * (6 - 4) * (6 - 5)) = sqrt(6 * 3 * 2 * 1) = sqrt(36) = 6
Таким образом, длина треугольника составляет 6 единиц длины.
В данных примерах мы использовали известные стороны треугольника и формулы для нахождения его длины. При решении задач на нахождение длины треугольника необходимо использовать соответствующие математические формулы и подсчитывать результаты внимательно.
Расчет длины треугольника может быть достаточно простым, если известны его стороны. Найдя значения всех сторон, можно воспользоваться формулой геометрии для расчета периметра треугольника. При этом следует учитывать, что в треугольнике сумма длин любых двух сторон всегда должна быть больше длины третьей стороны.
Если известны только углы треугольника и одна его сторона, можно воспользоваться тригонометрическими функциями (тангенс, синус, косинус) для расчета длины других сторон. При этом следует помнить о необходимости использования соответствующих единиц измерения углов (радианы или градусы).
Если треугольник является прямоугольным, то для нахождения длин его сторон можно использовать теорему Пифагора. Это позволяет упростить вычисления и получить более точный результат.
В общем случае, для более сложных треугольников без заранее известных данных, расчет длины треугольника может потребовать применения более сложных методов и формул. В таких случаях рекомендуется обратиться к специалисту или использовать специализированные программы или онлайн-калькуляторы для расчета геометрических фигур.