Векторы широко используются в различных областях науки и техники, включая физику, математику, графику и компьютерные науки. Они представляют собой важный инструмент для изучения и описания различных физических явлений и процессов.
Длина вектора - одна из основных характеристик, которая позволяет оценить его величину или мощность. В нашем примере рассмотрим трехмерное пространство, характеризуемое тремя координатами. Для определения длины вектора в этом пространстве необходимо знать его координаты или компоненты вдоль трех ортогональных осей.
Для расчета длины вектора воспользуемся формулой, известной как теорема Пифагора. Согласно этой формуле, длина вектора равна квадратному корню из суммы квадратов его компонентов. То есть, если вектор представлен координатами (x, y, z), то его длина (в) вычисляется по формуле: в = √(x² + y² + z²).
Методы вычисления длины вектора в пространстве

Существует несколько методов вычисления длины вектора:
| Метод | Описание |
|---|---|
| Геометрический метод | Основывается на определении длины вектора с помощью геометрических свойств пространства. В этом методе длина вектора вычисляется с использованием координат его конечной точки. |
| Алгебраический метод | Основывается на математическом определении вектора и его координат. Длина вектора вычисляется по формуле, учитывающей значения координат. |
| Скалярное произведение | Использует определение скалярного произведения векторов и его свойства для вычисления длины вектора. В этом методе длина вектора вычисляется как квадратный корень из скалярного произведения вектора на самого себя. |
Выбор метода зависит от задачи и доступной информации о векторе. Каждый метод имеет свои преимущества и недостатки, поэтому важно выбрать самый подходящий метод в конкретной ситуации.
При вычислении длины вектора необходимо учитывать его размерность и координаты. В пространстве размерностью больше трех методы вычисления длины вектора становятся более сложными и требуют особого подхода.
Важно запомнить, что длина вектора всегда является неотрицательным числом. Если вектор имеет нулевую длину, он называется нулевым вектором.
Геометрический подход к определению длины вектора

Представим вектор в виде столбца координат:
| x | y | z |
|---|---|---|
| x1 | y1 | z1 |
Для нахождения длины вектора необходимо использовать формулу:
длина = √(x1^2 + y1^2 + z1^2)
По этой формуле, чтобы найти длину вектора, нужно возвести каждую координату в квадрат, затем сложить полученные значения и извлечь квадратный корень. Таким образом, можно легко определить длину вектора в трехмерном пространстве.
Алгебраический способ нахождения длины вектора в пространстве
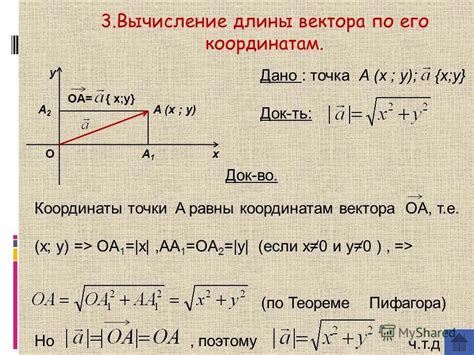
Для начала необходимо определиться с размерностью пространства, в котором задан вектор. Длина вектора в двумерном пространстве (плоскости) и в трехмерном пространстве (пространстве) находится по разным формулам. В данном случае рассмотрим трехмерный случай.
Пусть у нас есть вектор, заданный координатами (x, y, z). Для нахождения его длины можно воспользоваться формулой:
длина = √(x^2 + y^2 + z^2)
Таким образом, чтобы найти длину вектора, необходимо:
- Возвести в квадрат каждую из координат вектора.
- Сложить полученные квадраты.
- Извлечь квадратный корень из полученной суммы.
Выполнив эти простые математические операции, мы получим длину вектора в заданном пространстве. Алгебраический способ очень удобен, так как позволяет находить длину вектора в пространстве любой размерности.