Окружность - это геометрическая фигура, которая представляет собой множество точек, равноудаленных от одной фиксированной точки, называемой центром. Вокруг центральной точки окружности можно построить множество углов, но одним из наиболее важных из них является центральный угол.
Центральный угол - это угол, вершина которого является центром окружности, а стороны проходят через любую точку окружности. Градусная мера центрального угла определяется с помощью самого простого правила: 360 градусов равно полной окружности. Это значит, что центральный угол, охватывающий всю окружность, будет иметь градусную меру 360°.
Однако, если центральный угол охватывает только часть окружности, его градусная мера будет меньше 360°. Для расчета градусной меры центрального угла нужно знать длину дуги, которую он охватывает, и радиус окружности.
Определение градусной меры центрального угла

Центральным углом в окружности называется угол, вершина которого расположена в центре окружности, а его стороны проходят через две точки на окружности. Градусная мера центрального угла измеряется в градусах и определяет, насколько угол отклоняется от полного оборота, равного 360 градусов.
Для определения градусной меры центрального угла необходимо знать длину дуги (L) и радиус окружности (r). Градусная мера центрального угла (θ) может быть вычислена по формуле:
| Формула | Описание |
|---|---|
| θ = (L / (2πr)) * 360° | Градусная мера центрального угла |
Где π (пи) - это математическая константа, приближенно равная 3.14159.
Пример:
Пусть длина дуги L равна 10 см, а радиус окружности r - 5 см. Чтобы найти градусную меру центрального угла (θ), мы располагаем всей необходимой информацией для использования формулы:
| Длина дуги (L) | Радиус окружности (r) | Градусная мера центрального угла (θ) |
|---|---|---|
| 10 см | 5 см | (10 / (2π * 5)) * 360° ≈ 114.59° |
Таким образом, градусная мера центрального угла составляет примерно 114.59 градусов.
Центральный угол - что это?
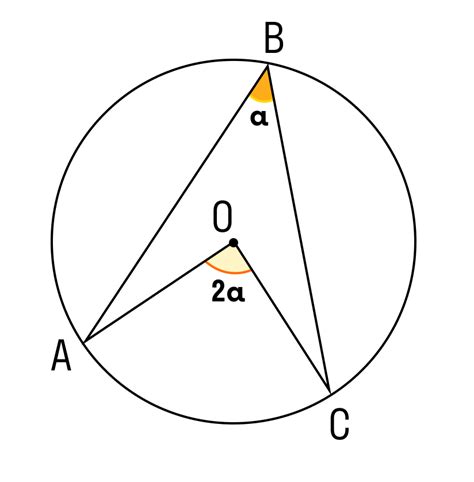
Градусная мера центрального угла равна длине дуги, которую он опирает, разделенной на радиус окружности и умноженной на 360 градусов.
Центральные углы широко используются в геометрии и тригонометрии для измерения и описания поворотов и вращений. Они также важны в различных областях науки и техники, таких как физика и инженерия, где применяются для определения угловых скоростей и направлений движения.
Найдя градусную меру центрального угла, мы можем определить его положение и описать его свойства, такие как величина, направление вращения и соотношения с другими углами.
Градусная мера центрального угла - как ее найти?
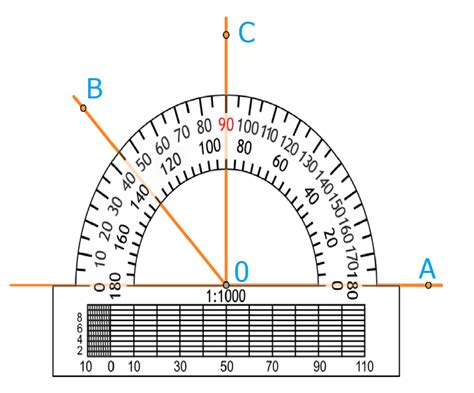
Основная формула для нахождения градусной меры центрального угла состоит из двух элементов: радиуса окружности и длины дуги, соответствующей этому углу. Градусная мера центрального угла можно найти с помощью следующей формулы:
Градусная мера = (Длина дуги / Длина окружности) * 360
При этом необходимо учесть, что длина окружности равна 2πR, где R - радиус окружности. Таким образом, формула может быть переписана следующим образом:
Градусная мера = (Длина дуги / (2πR)) * 360
Чтобы найти длину дуги, можно использовать другую формулу:
Длина дуги = (Градусная мера / 360) * (2πR)
Теперь, зная градусную меру и радиус окружности, мы можем расчитать длину дуги и наоборот.
Используя эти формулы, можно легко находить градусную меру центрального угла в окружности и обратно. Это позволяет проводить различные геометрические и математические расчеты, а также решать задачи, связанные с изучением фигур и окружностей.