Правильный десятиугольник – это многоугольник, состоящий из десяти равных сторон и десяти равных углов. Знание градусной меры углов в правильном десятиугольнике может быть полезно для различных математических и геометрических расчетов. Для определения градусной меры углов в правильном десятиугольнике следует использовать теорию и формулы, которые позволяют вычислить эту величину.
Для начала, важно знать, что сумма всех углов в любом правильном многоугольнике равна (n-2) × 180 градусов, где n – количество углов многоугольника. В случае правильного десятиугольника сумма углов равна (10-2) × 180 = 1440 градусов.
Чтобы найти градусную меру каждого угла в правильном десятиугольнике, нужно разделить сумму углов на количество углов. В нашем случае, 1440 градусов / 10 углов = 144 градуса – это градусная мера каждого угла в правильном десятиугольнике.
Изучение градусной меры правильного десятиугольника
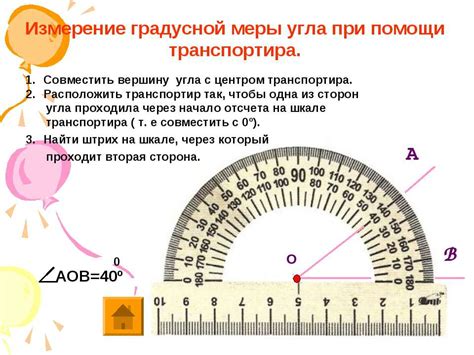
Для начала, нам следует понять, что правильный десятиугольник – это многоугольник, у которого все стороны и углы равны между собой. Градусная мера каждого угла правильного десятиугольника рассчитывается по формуле:
градусная мера = (180 × (10 − 2)) / 10
Давайте воспользуемся этой формулой для расчета градусной меры правильного десятиугольника:
| Количество сторон | Градусная мера |
|---|---|
| 10 | 144 |
Таким образом, для правильного десятиугольника градусная мера каждого угла составляет 144 градуса.
Изучение градусной меры правильного десятиугольника позволяет не только лучше понять его геометрические свойства, но и применять полученные знания в решении различных задач в области математики и физики.
Этапы изучения градусной меры:
Для понимания градусной меры правильного десятиугольника необходимо пройти несколько этапов:
- Определение градуса: Градус - это единица измерения углов. Один градус равен 1/360 части полного оборота.
- Понятие правильного десятиугольника: Правильный десятиугольник - это многоугольник, у которого все стороны и углы равны между собой.
- Сложение углов: Каждая сторона правильного десятиугольника образует угол в центре, который равен 360 градусов. Поэтому, чтобы найти градусную меру угла в правильном десятиугольнике, нужно разделить 360 на 10 (количество углов) и получить 36 градусов.
- Вычисление градусной меры каждого угла: В правильном десятиугольнике все углы равны между собой, поэтому градусная мера каждого угла равна 36 градусов.
Изучение градусной меры позволяет более глубоко понять геометрию и справляться с различными задачами, связанными с углами в правильных десятиугольниках.
Определение понятия "правильный десятиугольник"
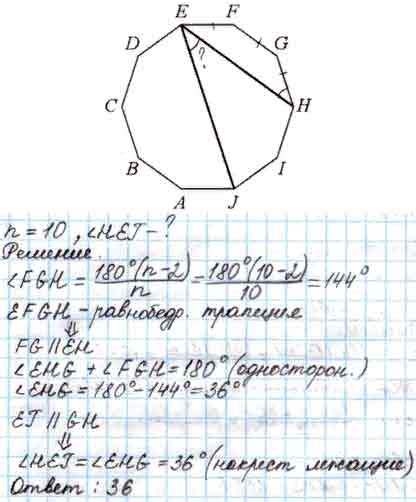
Каждый угол правильного десятиугольника имеет меру 144 градуса, так как сумма всех углов в десятиугольнике равна 1800 градусов (180 градусов умножается на 10).
Правильный десятиугольник обладает особыми свойствами, которые делают его уникальным и интересным для исследования. Например, его геометрические характеристики и свойства могут быть применены в различных областях, включая архитектуру, дизайн и науку.
Изучение правильных десятиугольников помогает развивать навыки в области геометрии и математики, а также способствует развитию воображения и логического мышления.
Основные свойства правильного десятиугольника
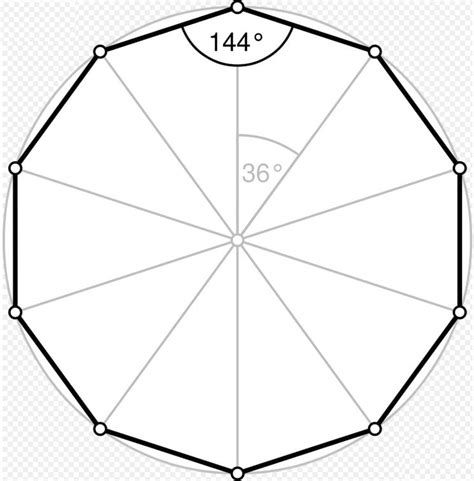
Основные свойства правильного десятиугольника:
- Равные стороны: все стороны правильного десятиугольника имеют одинаковую длину. Это означает, что если измерить одну сторону, можно использовать это значение для измерения всех остальных сторон.
- Равные углы: все углы правильного десятиугольника равны между собой и составляют 144 градуса каждый. Это следует из того факта, что сумма углов в десятиугольнике равна 1440 градусов.
- Симметричность: правильный десятиугольник обладает осью симметрии, которая проходит через центр фигуры. Это означает, что можно разделить десятиугольник на две равные части зеркально относительно этой оси.
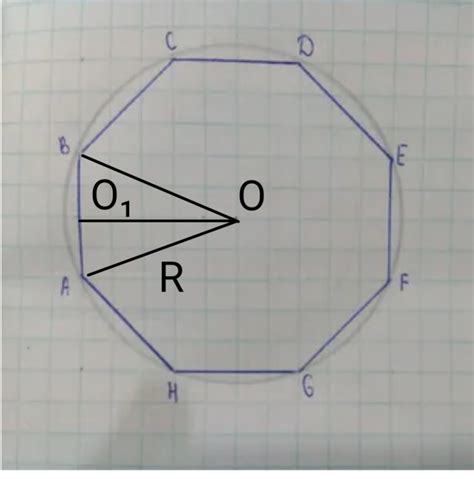
- Радиус: радиус правильного десятиугольника - это расстояние от центра фигуры до вершины или до середины стороны. Радиус можно выразить через длину стороны, используя формулу радиуса: R = s / (2 * sin(180° / 10)), где s - длина стороны.
- Площадь: площадь правильного десятиугольника можно вычислить по формуле: S = (5 * s^2) / (4 * tan(180° / 10)), где s - длина стороны.
- Периметр: периметр правильного десятиугольника можно вычислить, умножив длину стороны на 10, так как все стороны равны.
Знание основных свойств правильного десятиугольника помогает решать задачи по геометрии и подходить к исследованию других фигур на практике.
Нахождение угловых мер внутри правильного десятиугольника
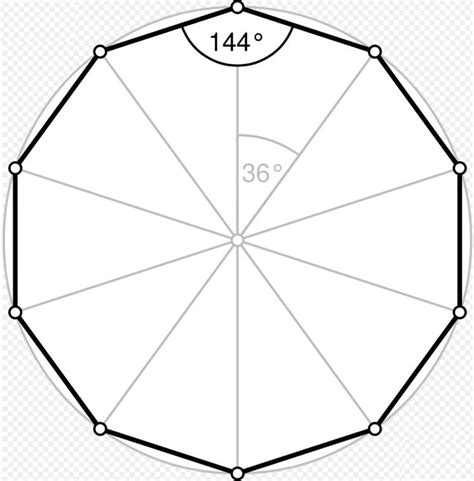
Чтобы найти угловую меру внутри правильного десятиугольника, нужно знать, что сумма всех углов внутри любого многоугольника равна (n-2) * 180 градусов, где n - количество углов.
Таким образом, для правильного десятиугольника сумма углов равна (10-2) * 180 = 1440 градусов.
Чтобы найти угловую меру одного угла внутри правильного десятиугольника, нужно разделить сумму углов на количество углов. В случае десятиугольника, один угол будет равен 1440 / 10 = 144 градусов.
Таким образом, каждый угол внутри правильного десятиугольника равен 144 градуса.
Использование формулы для расчета градусной меры угла правильного десятиугольника

Для расчета градусной меры угла правильного десятиугольника необходимо знать его количества углов и сумму градусных мер всех углов.
Правильный десятиугольник имеет 10 углов. Чтобы найти градусную меру одного угла, необходимо разделить сумму градусных мер всех углов на количество углов:
Градусная мера одного угла = Сумма градусных мер всех углов / Количество углов.
Так как у правильного десятиугольника сумма градусных мер всех углов равна 1800 градусов (10 углов по 180 градусов), то получаем:
Градусная мера одного угла = 1800 градусов / 10 углов = 180 градусов.
Итак, градусная мера угла правильного десятиугольника равна 180 градусов. Это означает, что все углы внутри десятиугольника равны 180 градусов.
Примеры задач и решений по нахождению градусной меры правильного десятиугольника
Задачи на нахождение градусной меры правильного десятиугольника могут быть разнообразными. Рассмотрим несколько примеров задач и их решений.
- Задача 1: Найдите градусную меру каждого угла в правильном десятиугольнике.
- Задача 2: Найдите градусную меру недостающего угла в правильном десятиугольнике, если известно, что сумма всех углов равна 1080 градусов.
- Задача 3: В правильном десятиугольнике ABCDEFGHIJ сторона AB равна 5 см. Найдите площадь десятиугольника.
Решение: Для нахождения градусной меры каждого угла в правильном десятиугольнике, нужно разделить сумму всех углов на количество углов. Градусная мера каждого угла в правильном десятиугольнике равна 360 градусов, деленная на 10, то есть 36 градусов.
Решение: Для нахождения градусной меры недостающего угла, нужно от суммы всех углов отнять градусную меру каждого из известных углов. В данной задаче, сумма всех углов равна 1080 градусов. В правильном десятиугольнике 10 углов, каждый угол равен 36 градусов. 10 * 36 = 360 градусов. Таким образом, градусная мера недостающего угла равна 1080 - 360 = 720 градусов.
Решение: Для нахождения площади правильного десятиугольника, нужно знать длину стороны и градусную меру каждого угла. В данной задаче известна длина стороны AB, равная 5 см. Также мы знаем, что все углы в правильном десятиугольнике равны. Градусная мера каждого угла равна 36 градусов (по решению первой задачи). Для нахождения площади десятиугольника можно воспользоваться формулой: S = (n * a^2) / (4 * tan(π/n)), где n - количество углов (в данной задаче 10), a - длина стороны. Подставляя известные значения, получаем: S = (10 * 5^2) / (4 * tan(π/10)). После вычислений получаем площадь десятиугольника.
Таким образом, нахождение градусной меры правильного десятиугольника в задачах может быть связано с нахождением суммы всех углов, нахождением недостающего угла или использованием формулы для нахождения площади. Все эти примеры задач и решений помогут вам лучше понять эту тему и научиться решать подобные задачи.