Линейные функции являются одними из самых простых и распространенных в математике. Они представляют собой прямые линии на координатной плоскости и широко применяются в различных областях науки и жизни.

Чтобы полностью определить линейную функцию, необходимо знать две точки на графике или координаты одной точки и угловой коэффициент функции. Угловой коэффициент (также называемый коэффициентом наклона) обозначается как k и определяет наклон прямой линии.

Для того чтобы найти угловой коэффициент линейной функции, вам понадобятся координаты двух точек на графике. Обозначим эти точки как (x1, y1) и (x2, y2). Угловой коэффициент можно вычислить по формуле:

k = (y2 - y1) / (x2 - x1)

После того, как у вас есть значение углового коэффициента, вы можете использовать любую из двух точек (x1, y1) или (x2, y2), чтобы найти интерсепт функции (пересечение линии с осью y). Интерсепт обозначается как b и может быть найден с использованием формулы:

b = y1 - k * x1

Теперь, когда у вас есть значения углового коэффициента и интерсепта, вы можете полностью определить линейную функцию и использовать ее для прогнозирования значений на графике или в других математических моделях.

Определение линейной функции

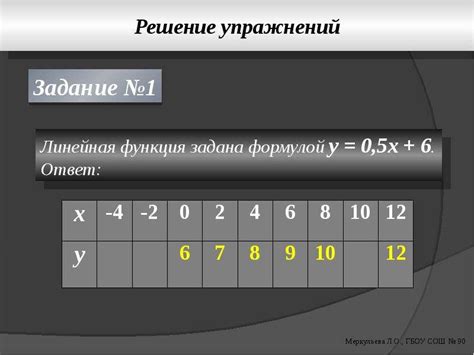
Коэффициент наклона (k) определяет угол, под которым прямая линия поднимается или опускается на графике. Если коэффициент положительный, линия будет идти вверх, если отрицательный - линия будет идти вниз.

Свободный член (b) является точкой, где линия пересекает ось ординат (ось значений y) на графике. Он указывает начальное значение функции, когда значение аргумента равно нулю.

Найдя коэффициенты линейной функции, мы можем определить, как она будет выглядеть на графике, а также использовать эту информацию для решения различных задач и задач на построение прямых линий.

Математические выражения для линейной функции

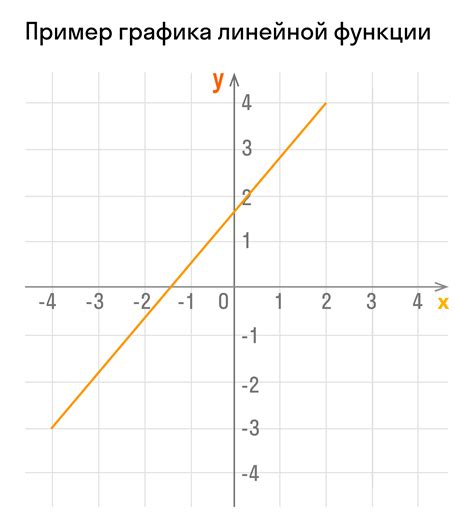
Линейная функция имеет вид y = mx + b, где:

• y - значение на оси ординат;
• x - значение на оси абсцисс;
• m - коэффициент наклона прямой, также называемый угловым коэффициентом;
• b - коэффициент смещения прямой, также называемый свободным членом.

Формула y = mx + b позволяет найти значение y при известном значении x. Для этого нужно подставить значение x в формулу и выполнить соответствующие математические операции.

Коэффициент наклона m показывает, насколько быстро изменяется значение y при изменении значения x. Если m положительный, то прямая идёт вверх, а если отрицательный, то прямая идёт вниз. Коэффициент смещения b определяет точку пересечения прямой с осью ординат.

Зная значения x и y для двух точек, можно найти значения коэффициентов m и b. Например, для точек (1, 3) и (4, 6) мы можем воспользоваться следующими формулами:

m = (y₂ - y₁) / (x₂ - x₁)

b = y₁ - mx₁

Где (x₁, y₁) и (x₂, y₂) - координаты двух точек. Подставив в формулы значения для наших точек, мы получим искомые значения коэффициентов.

Таким образом, используя математические выражения для линейной функции, можно определить угол наклона прямой и точку её пересечения с осью ординат, что помогает в решении разнообразных задач и построении графиков.

Выражение для y

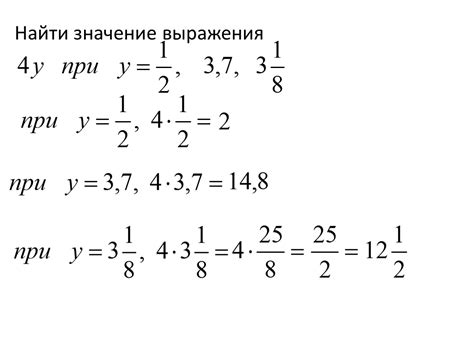
Выражение для y в линейной функции имеет вид:

• y = ax + b

где:

• y - значение функции, которое мы ищем
• a - коэффициент при переменной x (наклон прямой)
• x - значение аргумента функции
• b - свободный член (значение функции, когда x = 0)

Таким образом, чтобы найти значение функции y по известным значениям a, x и b, нужно подставить значения в выражение y = ax + b и выполнить вычисления.

Выражение для x

Чтобы найти выражение для переменной x в линейной функции, необходимо знать значения коэффициентов a и b, которые определяют уравнение прямой. Уравнение может быть записано в виде y = ax + b.

Для нахождения выражения для x нужно:

1. Из уравнения выразить x. Для этого нужно вычесть b из обеих частей уравнения:

• y - b = ax

• (y - b)/a = x

Таким образом, выражение для переменной x будет равно (y - b)/a. Оно позволяет определить значение x в линейной функции при заданном значении y. В таком выражении a является коэффициентом наклона прямой, а b - свободным членом уравнения.

Метод решения системы уравнений

Для нахождения коэффициентов линейной функции по координатам, необходимо решить систему уравнений, состоящую из двух уравнений. В общем виде система уравнений имеет вид:

• y = ax + b
• y = mx + d

где a, b, m и d - искомые коэффициенты линейной функции, x и y - известные координаты.

Для решения системы уравнений можно воспользоваться методом подстановки или методом исключения. В методе подстановки мы решаем одно уравнение относительно одной переменной, затем подставляем найденное значение в другое уравнение и находим вторую переменную.

1. Выбираем одно из уравнений и решаем его относительно одной переменной.
2. Подставляем найденное значение переменной в другое уравнение.
3. Решаем полученное уравнение и находим вторую переменную.
4. Подставляем значения переменных в исходные уравнения и проверяем их.

В методе исключения мы складываем или вычитаем уравнения так, чтобы одна из переменных сократилась, и решаем полученное уравнение относительно одной переменной.

1. Умножаем одно или оба уравнения на такие числа, чтобы коэффициенты при одной переменной стали равными.
2. Складываем или вычитаем уравнения так, чтобы одна из переменных сократилась.
3. Решаем полученное уравнение относительно одной переменной.
4. Подставляем найденное значение переменной в одно из исходных уравнений и находим вторую переменную.
5. Проверяем полученные значения, подставляя их в исходные уравнения.

После нахождения значений переменных можно записать искомую линейную функцию в виде y = ax + b, где a и b - найденные коэффициенты.

Примеры и практические задания

Для лучшего понимания процесса нахождения коэффициентов линейной функции по координатам, рассмотрим несколько примеров и выполним несколько практических заданий.

Пример 1:

Даны координаты двух точек на плоскости: A(2, 3) и B(4, 7). Найти уравнение прямой, проходящей через эти точки.

Решение:

Для нахождения уравнения прямой, проходящей через две точки, необходимо воспользоваться формулой y = kx + b, где k - коэффициент наклона прямой, b - коэффициент сдвига прямой по оси y.

Используя координаты точек A(2, 3) и B(4, 7), найдем значение коэффициента наклона прямой:

k = (y2 - y1) / (x2 - x1) = (7 - 3) / (4 - 2) = 4 / 2 = 2

Далее, подставим значения координат точки A(2, 3) в уравнение прямой y = kx + b и найдем значение коэффициента сдвига прямой:

3 = 2 * 2 + b

3 = 4 + b

b = -1

Уравнение прямой, проходящей через точки A(2, 3) и B(4, 7), будет иметь вид y = 2x - 1.

Практическое задание 1:

Даны координаты двух точек на плоскости: C(1, 5) и D(-2, 3). Найти уравнение прямой, проходящей через эти точки.

Практическое задание 2:

Даны координаты двух точек на плоскости: E(0, 0) и F(3, -2). Найти уравнение прямой, проходящей через эти точки.