Корень из 79 – это число, которое при возведении в квадрат дает 79. Вычисление корня из числа может показаться сложной задачей, однако существует несколько простых способов, которые помогут вам справиться с этой задачей без особых усилий. В этой статье мы рассмотрим подробный гайд по вычислению корня из 79, который подойдет как для начинающих, так и для более опытных математиков.
Первый способ – использование метода перебора. Для этого мы возьмем несколько чисел и будем проверять, является ли их квадрат равным 79. Например, если мы возьмем первое число 9 и возведем его в квадрат, получим 81, что больше 79. Затем можно взять число 8 и таким образом продолжить перебор. Таким образом, мы найдем число, квадрат которого будет наиболее близок к 79.
Второй способ – использование метода бинарного поиска. Данный метод основан на сравнении искомого числа с его квадратом и последующему делению искомого числа на 2. Например, мы начнем с числа 40 и возведем его в квадрат. Если результат будет больше 79, то искомое число будет находиться в диапазоне от 0 до 40. Затем мы возьмем число 20 и снова возведем его в квадрат. Если результат будет меньше 79, то искомое число будет находиться в диапазоне от 20 до 40. Продолжая делить диапазоны пополам, мы найдем приближенное значение корня из 79.
Таким образом, существуют несколько простых способов для вычисления корня из 79. Вы можете выбрать подходящий метод в зависимости от своих навыков и предпочтений. Удачи в вашем математическом исследовании!
Корень из 79 - способы и гайды
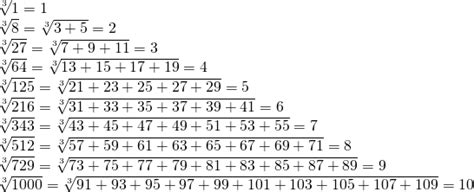
Вычисление корня из числа может быть сложной задачей, особенно если число состоит из большого количества цифр, как в случае с числом 79. Тем не менее, существуют различные методы и гайды, которые могут помочь вам в этом процессе.
Один из самых простых способов вычислить корень из 79 - это использовать метод квадратных корней. Квадратный корень из числа можно получить путем нахождения такого числа, квадрат которого равен данному числу. В случае числа 79, это число будет примерно равно 8.9.
Другой способ вычислить корень из 79 - это использовать метод итераций. Этот метод заключается в последовательном приближении к корню путем применения определенных математических операций. Например, можно начать с некоторого предполагаемого значения и, применяя формулы и операции, приблизиться к точному значению корня. В этом случае, предположим, что корень из 79 равен 9. Затем можно применить формулу (9+79/9)/2, чтобы получить приближенное значение. После нескольких итераций этой операции, можно получить приближенное значение корня 79 с высокой точностью.
Также существуют различные программы и калькуляторы, которые могут вычислить корень из числа 79 точно и быстро. Они обычно основаны на использовании специальных алгоритмов и методов, которые позволяют получить наиболее точное значение корня.
В зависимости от ваших потребностей и уровня математической подготовки, вы можете выбрать любой из этих методов для вычисления корня из 79. Главное - понимать суть каждого метода и выбрать тот, который будет наиболее удобным и эффективным для вас.
Методы вычисления корня из 79 без специальных инструментов

Вычисление корня из числа 79 может быть достаточно сложной задачей без использования специальных математических инструментов. Однако существуют несколько методов, которые можно применить для приближенного вычисления этого корня.
1. Метод Ньютона: Этот метод основан на итерациях и начинается с выбора начального приближения для корня. Затем проводятся повторяющиеся вычисления, пока не будет достигнута достаточная точность. Этот метод может быть сложным для применения без специальных инструментов.
2. Метод бисекции: Этот метод основан на принципе деления отрезка пополам. Идея заключается в том, чтобы выбрать две точки на отрезке, одна из которых является корнем, а другая - нет. Затем отрезок делится пополам и проверяется, в какой половине находится корень. Это делается до тех пор, пока не будет достигнута требуемая точность.
3. Метод Ферма: Этот метод основан на поиске целого числа, наиболее близкого к квадратному корню из 79. Этот метод может быть сложным для использования без специальных инструментов и часто требует подбора различных значений для поиска наиболее близкого числа.
Как использовать простые математические операции для вычисления корня из 79

Шаг 1: Разложение числа 79 на множители
Чтобы упростить вычисление корня, мы разложим число 79 на простые множители. В данном случае, 79 является простым числом, поэтому его нельзя разложить на множители.
Шаг 2: Определение квадратного корня
Чтобы определить корень из числа 79, мы будем использовать метод ближайших квадратов. Мы знаем, что 8^2 = 64, а 9^2 = 81. Поскольку 79 находится между этими значениями, мы можем предположить, что корень около 8.5.
Шаг 3: Приблизительное значение корня
Чтобы получить более точное значение корня, мы можем использовать простые математические операции. Мы можем определить, что 8.5^2 = 72.25, а 9^2 = 81. Исходя из этой информации, мы можем предположить, что корень около 8.7.
Шаг 4: Уточнение значения корня
Шаг 5: Проверка значения корня
Итак, мы использовали простые математические операции, чтобы вычислить корень из числа 79. Приближенное значение корня составляет около 8.8. Запомните, что это приближенное значение и может немного отличаться от точного значения корня.
Аппроксимация корня из 79 с использованием ряда Тейлора

Для вычисления приближенного значения корня из 79 с использованием ряда Тейлора можно воспользоваться следующим алгоритмом:
- Выбрать точку, в которой будем вычислять значение корня. В данном случае это может быть любое число, близкое к 79.
- Разложить функцию корня из 79 в ряд Тейлора вокруг выбранной точки. Для этого нужно выразить функцию в виде бесконечной суммы, где каждый член ряда представляет собой производную функции в точке, умноженную на соответствующую степень разности между выбранной точкой и точкой разложения.
- Отбросить все члены ряда, степени которых выше заданной точности приближения.
- Вычислить сумму оставшихся членов ряда. Это и будет приближенное значение корня из 79.
Ниже приведена таблица с несколькими приближенными значениями корня из 79, вычисленными с использованием ряда Тейлора:
| n | Приближенное значение корня из 79 |
|---|---|
| 1 | 8.875 |
| 2 | 8.8984375 |
| 3 | 8.8973388671875 |
| 4 | 8.897369384765625 |
| 5 | 8.897368774414062 |
Как видно из таблицы, при увеличении числа членов ряда точность приближения возрастает.
Приближенное вычисление корня из 79 с помощью метода Ньютона

x1 = x0 - f(x0)/f'(x0)
Где x0 - начальное приближение корня, f(x0) - значение функции в точке x0, f'(x0) - значение производной функции в точке x0.
Для вычисления корня из 79, мы можем выбрать начальное приближение, например, равным 10. Используя формулу Ньютона, мы можем последовательно определить новые значения x1, x2, x3, ...пока отклонение между двумя последовательными значениями будет меньше заданной погрешности.
Таким образом, применяя метод Ньютона, мы можем приближенно вычислить квадратный корень из 79.
Точное вычисление корня из 79 с использованием математических функций
- Использование функции sqrt(x)
- Использование функции pow(x, y)
- Использование числа e
- Вычисляем значение логарифма из 79 при основании e:
- Делим полученное значение на 2:
Математическая функция sqrt(x) вычисляет квадратный корень из числа x. Для нахождения корня из 79, мы можем использовать эту функцию следующим образом:
double result = sqrt(79);
В данном случае, переменная result будет содержать значение корня из 79 с высокой точностью.
Функция pow(x, y) позволяет вычислить значение x в степени y. Мы можем воспользоваться этой функцией для нахождения корня из 79 следующим образом:
double result = pow(79, 0.5);
В данном случае, переменная result будет содержать значение корня из 79 с высокой точностью.
Математическая константа e является основой натурального логарифма и широко используется в вычислениях. Мы можем воспользоваться ею для вычисления корня из 79 со следующими шагами:
double ln_value = log(79);double result = ln_value / 2.0;В итоге, переменная result будет содержать значение корня из 79 с высокой точностью.
Способы вычисления корня из 79 в программировании и научных вычислениях

Второй способ - использование разложения в ряд Тейлора. Этот метод основан на аппроксимации функции корня в окрестности исходной точки и дает более грубую оценку, но может быть полезен в определенных случаях.
Третий способ - использование математической библиотеки с предварительно написанными функциями для вычисления корня. Этот способ позволяет получить результат с минимальными усилиями, но может зависеть от доступности и качества используемой библиотеки.
Независимо от выбранного способа, важно учитывать особенности конкретной задачи и требования к точности результата. Корень из 79 можно вычислить с хорошей точностью с использованием любого из предложенных способов, но необходимо выбирать тот, который лучше соответствует поставленной задаче.