Корень комплексного числа – это одна из фундаментальных операций в математике, которая используется во многих областях, включая физику, инженерию и компьютерные науки. В основном, корень комплексного числа используется для решения уравнений и моделирования различных процессов.
Однако вычисление корня комплексного числа может быть достаточно сложной задачей, особенно при работе с большими и сложными числами. Традиционные методы, такие как метод Ньютона или метод деления пополам, могут быть неточными и требовательными к вычислительным ресурсам.
В последнее время, появилось несколько эффективных алгоритмов для вычисления корня комплексного числа, которые решают эти проблемы и позволяют получить более точные и быстрые результаты. Одним из таких алгоритмов является алгоритм Форстера, который использует преобразования Фурье и методы поиска. Этот алгоритм позволяет вычислить корень комплексного числа с высокой точностью и с относительно небольшими требованиями к вычислительным ресурсам.
Вычисление корня комплексного числа
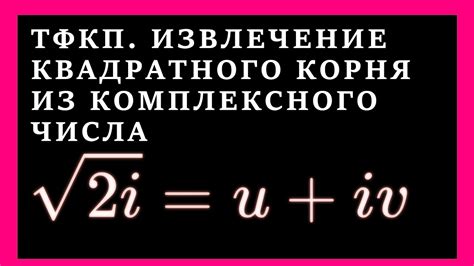
Один из самых популярных алгоритмов - метод Ньютона. Этот метод основан на итерационном процессе и позволяет быстро находить корень комплексного числа.
Суть метода Ньютона заключается в следующем: начиная с некоторого начального приближения, мы находим новое приближение, используя формулу:
xn+1 = xn - f(xn)/f'(xn)
где xn - текущее приближение, f(xn) - наше комплексное число, а f'(xn) - производная f(xn).
Мы продолжаем этот процесс до тех пор, пока разница между текущим и предыдущим приближениями не станет меньше некоторой заданной точности.
Еще один алгоритм - алгоритм Шура. Этот алгоритм основывается на теореме Шура из математического анализа. Он позволяет находить корень комплексного числа с высокой точностью.
Главным преимуществом алгоритма Шура является его эффективность и простота использования. Он также может быть применен к нелинейным уравнениям.
Использование таблиц и матриц часто упрощает процесс вычисления корня комплексного числа. Например, таблицы значений и производных функций могут быть использованы для составления приближений и уточнения этих приближений.
| Алгоритм | Описание |
|---|---|
| Метод Ньютона | Итерационный метод нахождения корня комплексного числа |
| Алгоритм Шура | Основывается на теореме Шура и обеспечивает высокую точность |
Методы вычисления корня комплексного числа

Вычисление корня комплексного числа представляет собой процесс нахождения другого комплексного числа, возведение которого в определенную степень дает исходное число.
Существует несколько методов для вычисления корня комплексного числа:
- Метод двоичного возведения в степень:
- Представим комплексное число в полярной форме, где модуль числа равен квадратному корню из суммы квадратов действительной и мнимой частей, а аргумент числа равен арктангенсу отношения мнимой и действительной частей.
- Возведем модуль числа в степень, разделим полученное число на количество корней, которое требуется найти, и возьмем квадратный корень из результата.
- Результат умножим на единичный вектор, повернутый на нужный угол, чтобы получить нужное количество корней исходного числа.
- Представим комплексное число в тригонометрической форме, где действительная часть числа равна модулю числа умноженному на косинус аргумента, а мнимая часть числа равна модулю числа умноженному на синус аргумента.
- Возведем модуль числа в степень и умножим результат на косинус степени умноженный на единичный вектор, а затем умножим модуль числа в степени на синус степени умноженный на перпендикулярный единичный вектор, чтобы получить новое комплексное число.
Оба этих метода позволяют находить корни комплексного числа эффективно. Выбор конкретного метода зависит от поставленной задачи и требуемой точности расчетов.
Эффективные алгоритмы вычисления корня комплексного числа

Корень комплексного числа представляет собой комплексное число, возведение которого в некоторую степень даёт исходное комплексное число. Для вычисления корня комплексного числа существуют несколько эффективных алгоритмов.
Одним из алгоритмов вычисления корня комплексного числа является формула Муавра. Она позволяет найти корень заданного комплексного числа, зная его модуль и аргумент.
Для вычисления корня комплексного числа по формуле Муавра необходимо:
- Выразить комплексное число в показательной форме, записав его модуль и аргумент.
- Разделить аргумент на число, равное степени корня, для получения аргумента искомого корня.
- Вычислить модуль искомого корня как корень из модуля заданного числа, возведённый в степень, равную обратной степени корня.
- Записать искомый корень в показательной форме.
Другим эффективным алгоритмом вычисления корня комплексного числа является метод Ньютона-Рафсона. Он позволяет приближённо найти корень комплексного числа с заданной точностью.
Для использования метода Ньютона-Рафсона для вычисления корня комплексного числа необходимо:
- Задать начальное приближение искомого корня.
- Вычислить следующее приближение корня по формуле: xn+1 = xn - f(xn) / f'(xn), где f(x) - функция, корнем которой является искомое число, f'(x) - производная функции f(x).
- Повторять шаг 2 до тех пор, пока не достигнута заданная точность.
Использование этих эффективных алгоритмов позволяет вычислять корень комплексного числа с высокой точностью и минимальными затратами вычислительных ресурсов.
Роль поиска в вычислении корня комплексного числа
Поиск играет важную роль в процессе вычисления корня комплексного числа, так как позволяет найти приближенное значение корня, которое можно использовать в дальнейших вычислениях. Он использует различные методы, такие как метод Ньютона или метод деления отрезка пополам, чтобы найти корень.
Одним из наиболее эффективных алгоритмов для вычисления корня комплексного числа является метод Ньютона. Он основан на принципе тангенциальной аппроксимации и позволяет находить корень с высокой точностью. В этом методе поиск играет решающую роль, так как он позволяет найти начальное приближение корня, которое будет использоваться в итерационном процессе вычисления.
Другой важный алгоритм для вычисления корня комплексного числа - метод деления отрезка пополам. В этом методе поиск также играет ключевую роль, так как он позволяет найти начальные границы отрезка, на котором будет проводиться деление. Затем происходит итеративное деление отрезка пополам до достижения требуемой точности.