Косинус и синус являются фундаментальными математическими функциями, которые широко применяются в различных областях науки и промышленности. Они находят применение не только в алгебре и геометрии, но и в физике, инженерии, компьютерных науках и многих других дисциплинах. Одной из самых распространенных задач, связанных с косинусом и синусом, является нахождение одного из них через другой в прямоугольном треугольнике.
Прямоугольный треугольник - это треугольник, у которого один из углов равен 90 градусам. В таком треугольнике можно определить три основных стороны: гипотенузу и две катеты. Гипотенуза - это самая длинная сторона, противолежащая прямому углу. Катеты - это две оставшиеся стороны, соединяющие концы гипотенузы с вершинами угла.
Формула косинуса через синус в прямоугольном треугольнике позволяет найти значение косинуса угла через известное значение синуса этого же угла и наоборот. Математически эта формула записывается так: косинус угла = катет / гипотенуза и синус угла = катет / гипотенуза. Это дает возможность легко находить значение одной из функций, если известно значение другой и соответствующие стороны треугольника.
Как вычислить косинус через синус в прямоугольном треугольнике?

Для прямоугольного треугольника, в котором один из углов равен 90 градусам, синус и косинус определяются следующим образом:
Синус угла:
Синус угла α в прямоугольном треугольнике вычисляется как отношение длины противолежащего катета (противоположного углу α) к гипотенузе (наибольшей стороне треугольника).
sin(α) = (противоположный катет) / (гипотенуза)
Косинус угла:
Косинус угла α в прямоугольном треугольнике вычисляется как отношение длины прилежащего катета к гипотенузе.
cos(α) = (прилежащий катет) / (гипотенуза)
Если нам известен синус угла, мы можем вычислить его косинус, используя соответствующую формулу. Например:
Пусть sin(α) = 0.6 (пример).
Тогда косинус угла α можно найти следующим образом:
cos(α) = √(1 - sin²(α))
cos(α) = √(1 - 0.6²) = √(1 - 0.36) = √0.64 = 0.8
Таким образом, косинус угла α равен 0.8.
Зная значения синуса и косинуса угла, мы можем использовать их для решения различных задач геометрии, включая вычисление сторон треугольника и углов между ними.
Определение косинуса и синуса
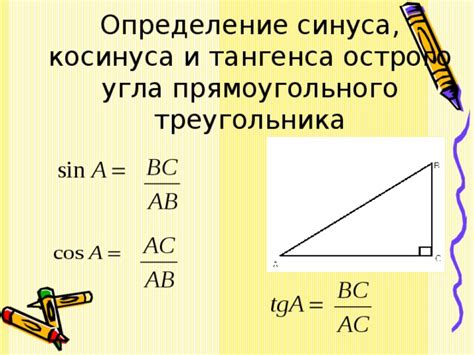
Косинус угла в прямоугольном треугольнике равен отношению длины прилежащего катета к длине гипотенузы. Косинус обозначается как cos.
Синус угла в прямоугольном треугольнике равен отношению длины противоположного катета к длине гипотенузы. Синус обозначается как sin.
Математические формулы для косинуса и синуса следующие:
- Косинус угла: cos(угол) = прилежащий катет / гипотенуза
- Синус угла: sin(угол) = противоположный катет / гипотенуза
Косинус и синус угла могут быть вычислены с помощью таблицы значений или с использованием тригонометрического круга. Они также имеют много свойств и идентичностей, которые можно использовать для решения задач в математике и физике.
Использование косинуса и синуса позволяет нам выяснить относительные углы и длины сторон прямоугольных треугольников, а также решать множество других задач, связанных с тригонометрией.
Геометрическая интерпретация косинуса через синус
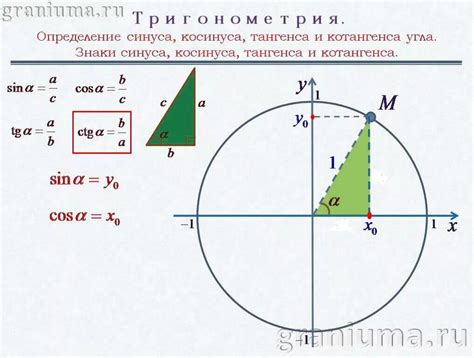
Интересно, что геометрическая интерпретация косинуса через синус также основывается на свойствах прямоугольного треугольника. Для того чтобы установить эту связь, воспользуемся теоремой Пифагора.
| Гипотенуза | Прилежащий катет | Противоположный катет | |
| Формула | c | a | b |
| Соотношение | c2 = a2 + b2 | c = a / cos(α) | c = b / sin(α) |
Используя теорему Пифагора, мы можем сформулировать следующее соотношение:
a2 + b2 = c2
Делим обе части этого уравнения на c2 и получаем:
a2/c2 + b2/c2 = 1
Заменяя a/c на cos(α) и b/c на sin(α), получаем:
cos2(α) + sin2(α) = 1
Это равенство, известное как тригонометрическое тождество, доказывает геометрическую интерпретацию косинуса через синус. Оно подтверждает, что синус и косинус угла всегда связаны друг с другом в прямоугольном треугольнике, независимо от его размеров.
Математическое выражение косинуса через синус
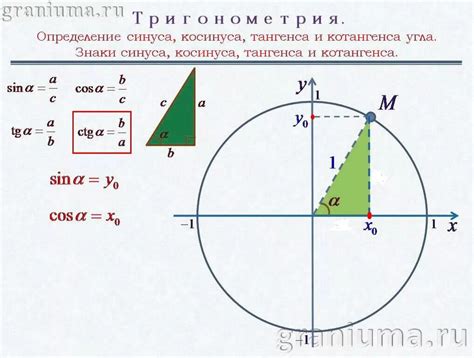
Для прямоугольного треугольника с гипотенузой (сторона против напротив прямого угла) равной c, катетами (стороны, прилегающие к прямому углу) равными a и b можно выразить соответствующие углы. Синус угла α (против катета a) определяется как отношение противолежащего катета к гипотенузе: sin(α) = a / c. Косинус угла α (против катета a) определяется как отношение прилегающего катета к гипотенузе: cos(α) = b / c.
Косинус также может быть выражен через синус, используя теорему Пифагора, которая утверждает, что сумма квадратов катетов равна квадрату гипотенузы: a2 + b2 = c2. Используя эту теорему, мы можем выразить косинус как: cos(α) = sqrt(c2 - a2) / c.