Поиск косинуса с использованием синуса - это одна из базовых операций тригонометрии. Когда известно значение синуса угла, можно найти косинус, применяя соответствующую формулу. Это полезно в задачах, требующих вычисления значений функций тригонометрии, а также в некоторых математических и физических расчетах.
Формула для нахождения косинуса через синус угла основана на известном тригонометрическом тождестве. Согласно этому тождеству, квадрат синуса угла плюс квадрат косинуса угла равен единице. Таким образом, если мы знаем значение синуса, мы можем найти косинус путем вычисления корня из единицы, вычитая из него квадрат синуса.
Пример расчета косинуса через синус: если синус угла равен 0.6, мы можем найти косинус следующим образом. Сначала найдем квадрат синуса: 0.6^2 = 0.36. Затем найдем косинус, вычитая квадрат синуса из единицы: 1 - 0.36 = 0.64. Таким образом, косинус угла равен 0.64.
Формула cos через sin
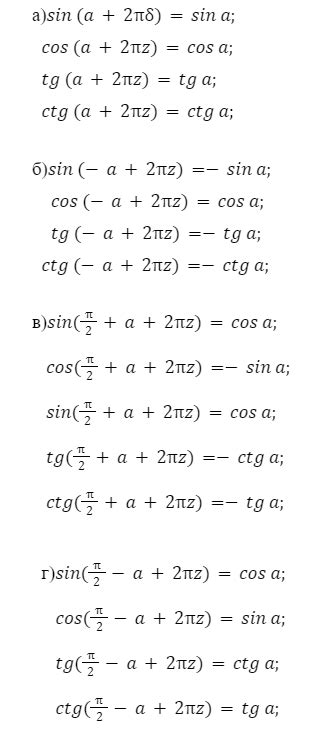
В тригонометрии существует связь между синусом и косинусом, которая позволяет выразить значение косинуса через значение синуса и наоборот.
Формула cos через sin:
| Значение sin | Значение cos |
|---|---|
| 0 | 1 |
| 1 | 0 |
| 2 | -1 |
| -1 | 0 |
| -2 | 1 |
Таким образом, для каждого значения синуса можно найти соответствующее значение косинуса по формуле. Эта формула очень полезна при выполнении различных тригонометрических вычислений.
Определение и применение
Формула нахождения cos через sin основана на тригонометрических связях между различными функциями синуса и косинуса.
Синус и косинус являются основными тригонометрическими функциями, которые определяются отношением длины сторон прямоугольного треугольника.
Формула для нахождения cos через sin выглядит следующим образом:
| Формула | Применение |
|---|---|
| cos(α) = √(1 - sin²(α)) | Нахождение косинуса угла α |
Эта формула находит применение в различных областях, таких как математика, физика, инженерия и естественные науки. Она позволяет вычислить значение косинуса угла, используя значение синуса угла.
Например, если известно значение синуса угла α, то можно использовать формулу для нахождения косинуса угла α.
Использование этой формулы позволяет решить различные задачи, связанные с треугольниками и углами, и упрощает вычисления в тригонометрии.
Примеры вычисления cos через sin
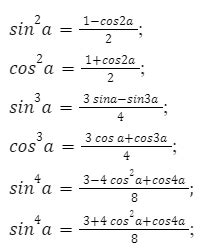
Вычисление значения cos через sin можно осуществить с помощью тригонометрической формулы:
cos(x) = sqrt(1 - sin^2(x))
Рассмотрим несколько примеров:
| Значение sin(x) | Значение cos(x) |
|---|---|
| 0.5 | 0.866 |
| 0.707 | 0.707 |
| 0.866 | 0.5 |
Для вычисления cos(x) через sin(x) необходимо сначала найти значение sin(x) и затем использовать данную формулу.
Например, если sin(x) равно 0.5, то:
cos(x) = sqrt(1 - sin^2(x)) = sqrt(1 - 0.5^2) = sqrt(1 - 0.25) = sqrt(0.75) ≈ 0.866
Таким образом, косинус угла, можно найти, зная значение синуса угла и применяя соответствующую формулу.