Косинус треугольника - это математическое понятие, которое используется для определения углов в треугольнике. Когда известны длины всех трех сторон треугольника, можно использовать формулу косинуса для определения значений углов.
Формула косинуса треугольника выглядит следующим образом:
cos(A) = (b^2 + c^2 - a^2) / (2bc)
Где A - это один из углов треугольника, a, b и c - длины сторон треугольника, соответствующие этому углу.
Теперь, когда у нас есть формула, давайте рассмотрим ее более подробно. В числителе формулы мы складываем квадраты длин двух сторон треугольника и вычитаем квадрат длины третьей стороны. Затем результат делится на произведение длин двух сторон, участвующих в числителе формулы.
Полученное значение косинуса используется для нахождения значения угла A. При необходимости можно использовать обратную функцию косинуса (арккосинус), чтобы найти сам угол.
Использование формулы косинуса треугольника с известными сторонами является полезным инструментом при решении задач в геометрии и тригонометрии. Она позволяет нам определить углы треугольника, имея только длины его сторон. Это особенно полезно, когда необходимо решить задачу, связанную с построением фигуры или вычислением ее геометрических характеристик.
Что такое косинус?

Косинус угла обозначается как cos и выражается следующей формулой:
cos(θ) = A/H
где θ – угол, A – длина прилежащего катета, H – длина гипотенузы.
Значение косинуса всегда находится в диапазоне от -1 до 1. Если косинус равен 1, то угол равен 0 градусов или косинус равен 0, то угол равен 90 градусов. Если косинус отрицательный, то угол находится во втором или третьем квадранте.
Косинус часто используется в геометрии, физике и инженерии для решения задач, связанных с треугольниками, векторами и колебаниями. Математический аппарат косинуса также широко применяется в обработке сигналов, статистике и других научных дисциплинах.
Понятие косинуса
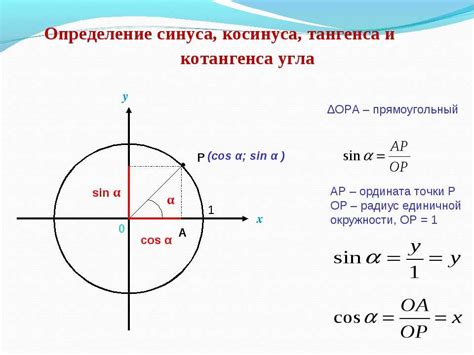
Косинус обозначается символом cos и может принимать значения от -1 до 1.
В математике и физике косинус находит широкое применение, включая решение уравнений, вычисление расстояний и определение направлений.
| Угол | Косинус угла |
|---|---|
| 0° | 1 |
| 30° | √3/2 |
| 45° | 1/√2 |
| 60° | 1/2 |
| 90° | 0 |
Знание значения косинуса угла позволяет находить углы треугольника, если известны длины его сторон, а также находить стороны треугольника, если известны угол и одна из сторон.
Косинус треугольника: формула
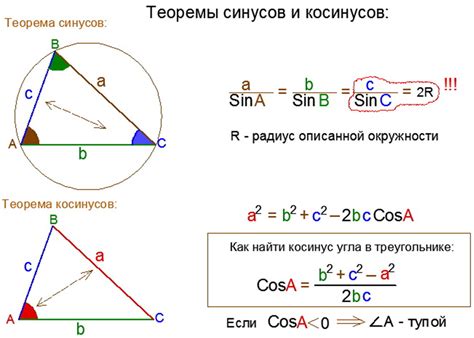
Формула для вычисления косинуса треугольника основана на теореме Пифагора и может быть записана следующим образом:
cos A = (b^2 + c^2 - a^2) / (2bc)
где A - угол при гипотенузе, a - длина гипотенузы, b и c - длины катетов.
Эта формула позволяет нам найти значение косинуса треугольника, а затем использовать его для определения углов с помощью обратной функции косинуса.
Формула косинуса треугольника
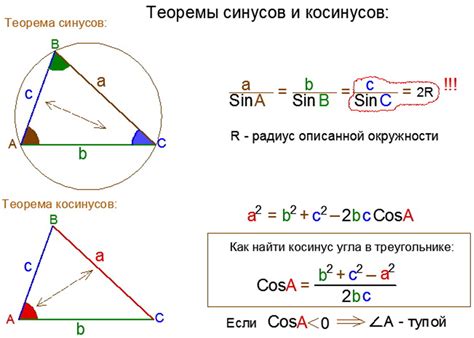
Формула косинуса треугольника имеет следующий вид:
cos(A) = (b^2 + c^2 - a^2) / (2 * b * c)
где:
- A - угол треугольника, для которого мы хотим вычислить косинус;
- a, b, c - длины сторон треугольника.
Важно отметить, что формула косинуса треугольника работает только для треугольников, в которых известны длины всех трех сторон.
Используя формулу косинуса треугольника, мы можем вычислить косинус любого угла треугольника, если известны длины его сторон. Это может быть полезно при решении задач, связанных с нахождением углов треугольника или проверкой его геометрических свойств.
Известные стороны треугольника
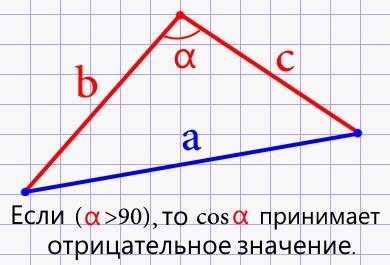
Для вычисления косинуса треугольника с известными сторонами необходимо знать длины всех трех сторон треугольника, обозначим их как a, b и c.
Затем можно воспользоваться формулой для косинуса треугольника:
| Формула для косинуса: | cos(A) = (b^2 + c^2 - a^2) / (2*b*c) |
|---|---|
| cos(B) = (a^2 + c^2 - b^2) / (2*a*c) | |
| cos(C) = (a^2 + b^2 - c^2) / (2*a*b) |
Здесь A, B и C соответствуют углам треугольника, противоположным сторонам a, b и c соответственно.
Результатом вычислений будет косинус каждого угла треугольника.
Зная косинусы углов, можно рассчитать значение синуса для каждого угла с помощью тригонометрической формулы sin^2(A) + cos^2(A) = 1.
Вычисление косинуса по известным сторонам

Формула для вычисления косинуса треугольника, известными сторонами которого являются a, b и c, имеет вид:
cos(C) = (a^2 + b^2 - c^2) / (2ab)
Где C – угол противоположный стороне c. Применяется тождество тригонометрии, известное как закон косинусов.
Чтобы вычислить косинус треугольника по известным сторонам, необходимо подставить значения сторон a, b и c в формулу и выполнить соответствующие математические операции.
Зная значение косинуса треугольника, можно использовать его для различных вычислений, например для определения других углов треугольника или для нахождения площади треугольника.