Косинус треугольника - это величина, которая позволяет нам определить угол между двумя сторонами треугольника. Она играет важную роль в геометрии, физике и других научных областях. Для расчета косинуса треугольника мы используем специальную формулу, которую можно выразить через длины сторон треугольника.
Формула косинуса треугольника выглядит следующим образом: cos(A) = (b^2 + c^2 - a^2) / (2bc), где A - угол между сторонами b и c, a - сторона, противолежащая углу A, b и c - длины соответствующих сторон треугольника.
Существуют различные методы расчета косинуса треугольника. Один из таких методов - метод с использованием тригонометрических функций. Например, если известны длины всех трех сторон треугольника, мы можем использовать формулу косинуса для расчета углов треугольника.
Другой метод рассчитывает косинус треугольника с помощью координат точек, задающих его вершины. В этом случае необходимо использовать формулу косинуса треугольника, которая основана на нахождении скалярного произведения векторов, образованных сторонами треугольника.
Вводная информация о косинусе треугольника
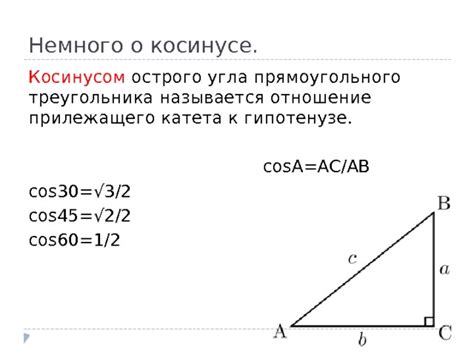
Косинус треугольника часто обозначается символом cos и выражается в виде:
cos(α) = Adjacent / Hypotenuse
где α - угол, Adjacent - длина прилежащего катета, Hypotenuse - длина гипотенузы.
Косинус треугольника имеет широкий спектр применения. Он позволяет находить значения углов и сторон треугольника, а также решать задачи, связанные с тригонометрическими функциями. Кроме того, косинус треугольника является основой для расчета других тригонометрических функций, таких как синус и тангенс.
Что такое косинус треугольника?
Математический символ для обозначения косинуса треугольника - cos.
Косинус треугольника может быть вычислен по формуле:
cos(A) = Adjacent / Hypotenuse
где A - угол между гипотенузой и прилегающим катетом, Adjacent - длина прилегающего катета, а Hypotenuse - длина гипотенузы.
Зная значения двух из этих величин, можно вычислить третью, используя данную формулу.
Косинус треугольника имеет много приложений в различных областях, таких как геометрия, физика, инженерия и астрономия. Он позволяет определить углы и стороны треугольников, что является важным для решения различных задач и задач с использованием тригонометрии.
Зачем нужно знать косинус треугольника?

Одним из основных применений косинуса треугольника является вычисление длин сторон треугольника по известным углам и одной из сторон. Это особенно полезно при работе с неравносторонними треугольниками, где нельзя использовать простые геометрические свойства для расчета.
Косинус треугольника также используется при решении треугольных неравенств, определении площади треугольника, нахождении высоты и многих других задачах. Он помогает определять углы и отношения между сторонами треугольника, что позволяет более точно анализировать и измерять форму и свойства треугольника.
Важно отметить, что косинус треугольника часто используется в связке с другими тригонометрическими функциями, такими как синус и тангенс, для более полного анализа треугольника и его свойств. Знание косинуса треугольника позволяет более точно моделировать и предсказывать поведение и взаимодействие геометрических объектов.
Таким образом, знание косинуса треугольника является необходимым для решения различных геометрических и физических задач, а также для проведения точных измерений и анализа объектов в разных научных областях.
Формула для расчета косинуса треугольника
Формула для расчета косинуса треугольника может быть записана следующим образом:
cos(A) = (b² + c² - a²) / (2bc)
где А - угол между сторонами b и c, а a - противолежащая этому углу сторона треугольника.
Данная формула представляет собой одну из основных формул для вычисления косинуса треугольника и является важной частью геометрии и тригонометрии. Она позволяет определить значение косинуса треугольника по известным значениям длин его сторон и углу между ними.
Расчет косинуса треугольника с помощью данной формулы позволяет определить величину угла между сторонами треугольника и использовать ее для решения различных геометрических и технических задач, включая построение треугольников, нахождение длины стороны треугольника и вычисление площади треугольника.
Использование формулы для расчета косинуса треугольника позволяет упростить и сделать более точными различные геометрические и технические расчеты, а также помогает в решении широкого спектра задач, связанных с треугольниками.
Как выразить косинус треугольника через его стороны?
Косинус треугольника может быть выражен через его стороны с помощью формулы косинусов. Формула косинусов основана на теореме косинусов и позволяет найти косинус угла треугольника, зная длины его сторон.
Формула косинусов имеет следующий вид:
- cos(A) = (b^2 + c^2 - a^2) / (2 * b * c)
- cos(B) = (a^2 + c^2 - b^2) / (2 * a * c)
- cos(C) = (a^2 + b^2 - c^2) / (2 * a * b)
Где A, B, C – углы треугольника, a, b, c – длины его сторон. Косинус каждого угла треугольника можно выразить с помощью этой формулы.
Расчет косинуса треугольника через его стороны может быть полезен при решении различных геометрических задач, включая построение треугольника по его сторонам или нахождение углов треугольника по известным сторонам.
Как использовать формулу для расчета косинуса треугольника?

Формула для расчета косинуса треугольника зависит от информации, доступной о треугольнике. Основные методы расчета косинуса в треугольнике включают:
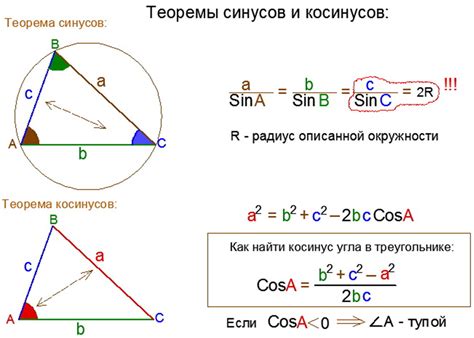
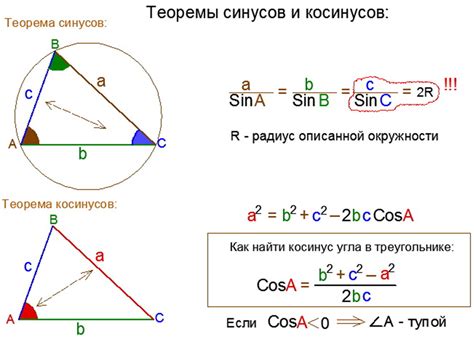
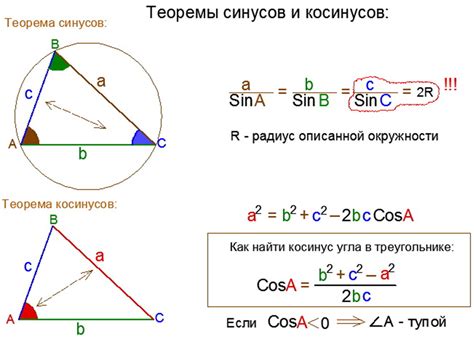
- Использование теоремы косинусов: $cos(A) = \frac{b^2 + c^2 - a^2}{2bc}$, где $A$ - угол противоположный стороне $a$, $a$, $b$, $c$ - длины сторон.
- Использование теоремы синусов: $cos(A) = sin(B) \cdot sin(C) + cos(B) \cdot cos(C) \cdot cos(a)$, где $A$ - угол противоположный стороне $a$, $a$, $b$, $c$ - длины сторон.
- Использование геометрических свойств: косинус угла можно выразить через отношение длины высоты, опущенной на сторону треугольника, к длине этой стороны.
Выбор конкретного метода расчета зависит от известной информации о треугольнике и задачи, которую нужно решить. Важно помнить, что косинус может быть выражен как в радианах, так и в градусах, поэтому необходимо учитывать это при выборе формулы и преобразовании результатов.
Правильное использование формулы для расчета косинуса треугольника позволяет определить значения углов или сторон треугольника, что может быть полезно при решении различных геометрических и научных задач. Важно быть внимательным при вводе данных и использовать углы и стороны с правильными знаками и единицами измерения.
Методы расчета косинуса треугольника
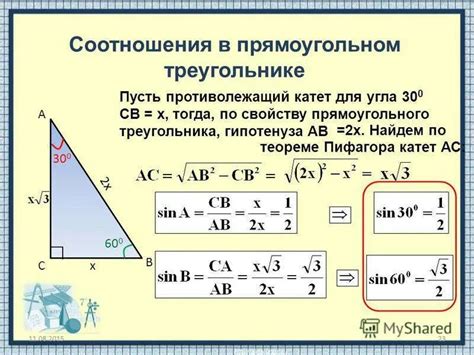
Формула косинуса: Используется, когда известны длины всех трех сторон треугольника. Формула выглядит следующим образом:
cos(A) = (b^2 + c^2 - a^2) / (2 * b * c)
где A - угол, противолежащий стороне a, b и c - длины сторон треугольника.
Теорема косинусов: Применяется, когда известны длины двух сторон и между ними заключен угол. Теорема состоит в следующем:
c^2 = a^2 + b^2 - 2ab * cos(C)
где c - длина стороны, противолежащей углу C, a и b - длины других двух сторон треугольника.
Теорема синусов: Применяется, когда известна длина одной стороны и два угла, заключенных между ней и другими сторонами треугольника. Теорема записывается следующим образом:
sin(A) / a = sin(B) / b = sin(C) / c
где A, B и C - углы, a, b и c - длины сторон треугольника.
Выбор метода для расчета косинуса треугольника зависит от данных, которые нам известны. Зная конкретные значения сторон и углов, можно применить соответствующую формулу для определения косинуса треугольника. Это позволяет нам точно вычислить его значение и использовать его в последующих расчетах или задачах геометрии.
Геометрический метод расчета косинуса треугольника
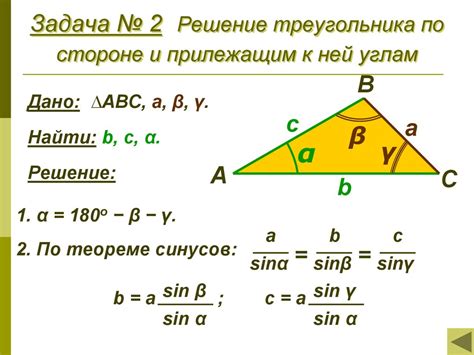
Геометрический метод основан на использовании теоремы косинусов. Согласно этой теореме, косинус угла треугольника равен отношению суммы квадратов длин двух сторон, их разности и произведения длин тех же сторон. Формулу для расчета косинуса можно записать следующим образом:
cos(угол) = (a^2 + b^2 - c^2) / (2ab)
Где a, b и c - длины сторон треугольника, а угол - один из его углов.
Для использования геометрического метода расчета косинуса треугольника необходимо знать длины его сторон. После подстановки значений в формулу можно вычислить косинус угла. Полученное значение позволит определить величину и характер угла - острый, прямой или тупой.
Геометрический метод расчета косинуса треугольника удобен для решения различных геометрических задач, связанных с треугольниками. Он позволяет определить все углы треугольника, используя только его стороны. Правильное использование этого метода поможет проводить точные измерения углов, а также решать задачи, связанные с тригонометрией.
Тригонометрический метод расчета косинуса треугольника
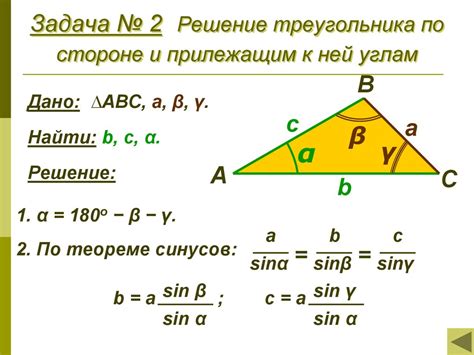
Тригонометрический метод расчета косинуса треугольника основывается на использовании соотношений между сторонами и углами треугольника. Косинус треугольника представляет собой отношение длины прилежащего к данному углу катета к гипотенузе.
Формула для вычисления косинуса треугольника с помощью тригонометрического метода выглядит следующим образом:
cos(A) = a / c
где cos(A) - косинус угла A, a - длина прилежащего к углу A катета, c - длина гипотенузы треугольника.
Для вычисления косинуса треугольника необходимо знать длины сторон треугольника и значения углов. После подстановки значений в формулу, можно легко вычислить косинус треугольника и получить его числовое значение.
Тригонометрический метод расчета косинуса треугольника является одним из базовых методов в тригонометрии и находит широкое применение в различных областях, включая геометрию, физику и инженерные расчеты.