Косинус – одна из основных тригонометрических функций, которая широко используется в геометрии и математике. Очень важно понимать, как вычислять косинус угла, особенно когда дело касается треугольников с непрямыми углами. В этой статье мы рассмотрим формулу косинуса для треугольников с непрямым углом и расскажем о различных способах его вычисления.
Косинус угла в треугольнике с непрямым углом можно представить как отношение длины стороны, прилегающей к данному углу, к гипотенузе треугольника. Формула для вычисления косинуса угла в треугольнике с непрямым углом выглядит следующим образом: cos(A) = b/c, где A – мера непрямого угла, b – длина стороны, прилегающей к углу, и с – длина гипотенузы.
Существует несколько способов вычисления косинуса угла в треугольнике с непрямым углом. Один из самых распространенных способов – использование таблиц и калькуляторов с тригонометрическами функциями. В табличной форме косинусы углов обычно представлены для углов от 0 до 90 градусов с шагом 1 градус. Однако, в случае треугольников с непрямыми углами, точное значение косинуса может быть сложно найти в таблице, поскольку оно зависит от угла, а также от длин сторон треугольника. Поэтому иногда требуется использовать методы вычисления косинуса угла с помощью интерполяции или численных методов.
Что такое косинус треугольника?
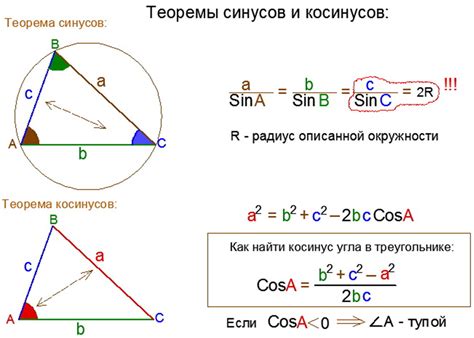
В треугольнике, косинус угла определяется, как отношение длины прилежащего к углу катета к длине гипотенузы. Можно представить косинус треугольника в виде отношения катета к гипотенузе или использовать формулу, где косинус равен отношению смежного катета к гипотенузе.
Косинус треугольника обычно обозначается как cos и может быть вычислен с помощью тригонометрических таблиц или калькулятора с тригонометрическими функциями. Также существуют специальные формулы и способы вычисления косинуса треугольника, которые можно использовать для нахождения его значения в конкретном случае.
Определение и особенности
Основная особенность косинуса треугольника с непрямым углом заключается в том, что значение функции всегда лежит в диапазоне от -1 до 1. Когда непрямой угол треугольника равен 90 градусов, косинус равен 0, что означает, что сторона, прилегающая к этому углу, является гипотенузой треугольника.
Косинус также позволяет определить отношение длин стороны, прилежащей к острым углам треугольника, к гипотенузе. Зная значения косинусов углов треугольника, можно определить длины сторон и углы треугольника с помощью тригонометрических формул и правил.
Формула для вычисления косинуса треугольника
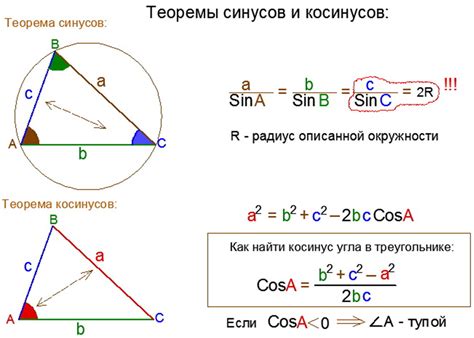
cos(Угол) = сторона / гипотенуза
В этой формуле косинус угла определяется как отношение длины стороны треугольника к длине его гипотенузы. Косинус треугольника может быть вычислен для любого угла треугольника, включая непрямые углы.
Для использования формулы вычисления косинуса треугольника, необходимо знать длины сторон треугольника и угол, для которого вы хотите вычислить косинус. После подстановки значений в формулу вы получите числовое значение косинуса треугольника с непрямым углом.
Формула для вычисления косинуса треугольника является основой для различных математических и физических вычислений, связанных с треугольниками и углами. Это полезный инструмент для решения разнообразных задач, связанных с геометрией и тригонометрией.
Связь косинуса с другими тригонометрическими функциями

Связь косинуса с синусом и тангенсом задается следующими формулами:
- cos(x) = sin(90° - x)
- cos(x) = 1 / tan(x)
Первая формула показывает, что косинус угла равен синусу дополнительного угла, то есть угла, который дополняет данный угол до 90 градусов. Это следует из свойства, что сумма угла и его дополнительного угла составляет прямой угол, который равен 90 градусам.
Вторая формула показывает, что косинус угла равен обратному значению тангенса угла. Тангенс угла определяется как отношение противолежащего катета к прилежащему катету и обратно пропорционален косинусу угла.
Зная связь косинуса с синусом и тангенсом, можно использовать эти формулы для вычисления значений тригонометрических функций в различных задачах и применений.
Вычисление косинуса треугольника через стороны

Косинус треугольника с непрямым углом можно вычислить, зная длины его сторон. Для этого применяется теорема косинусов, которая устанавливает связь между сторонами треугольника и косинусами его углов.
Формула для вычисления косинуса треугольника через стороны выглядит следующим образом:
cos(C) = (a^2 + b^2 - c^2) / (2ab)
где C - непрямой угол треугольника, a и b - длины сторон треугольника, c - длина противолежащей непрямому углу стороны.
Для вычисления косинуса треугольника нужно:
- Найти длины всех сторон треугольника.
- Вставить значения длин сторон в формулу для вычисления косинуса.
- Решить полученное уравнение и получить значение косинуса.
После этого можно использовать полученное значение косинуса для решения задач по тригонометрии или для нахождения других параметров треугольника.
Пример вычисления косинуса треугольника через стороны:
Допустим, у нас есть треугольник ABC с известными сторонами a = 5, b = 6 и c = 8. Чтобы найти косинус непрямого угла C, вставим значения сторон в формулу:
cos(C) = (5^2 + 6^2 - 8^2) / (2 * 5 * 6)
После простых вычислений получаем:
cos(C) = (25 + 36 - 64) / 60
cos(C) = -3 / 60
cos(C) = -0.05
Таким образом, косинус непрямого угла C равен -0.05.
Вычисление косинуса треугольника через стороны может быть полезно в решении различных геометрических и технических задач, а также при изучении тригонометрии и построении треугольников.
Как определить стороны треугольника
Чтобы определить стороны треугольника, необходимо знать его углы и длину одной из сторон. Рассмотрим несколько способов вычисления сторон треугольника.
1. Использование теоремы косинусов:
Если известны длины двух сторон треугольника и между ними известен угол, то третью сторону можно вычислить с помощью теоремы косинусов. Формула для вычисления стороны треугольника по теореме косинусов выглядит следующим образом:
c^2 = a^2 + b^2 - 2ab * cos(C)
где a и b - длины известных сторон треугольника, C - известный угол между этими сторонами, а c - длина третьей стороны, которую необходимо вычислить. После применения формулы, можно найти значение стороны c.
2. Использование соотношений в прямоугольном треугольнике:
Если треугольник прямоугольный, то длины его сторон можно определить, используя соотношения в прямоугольном треугольнике, такие как:
a^2 = b^2 + c^2
b^2 = a^2 + c^2
c^2 = a^2 + b^2
где a, b и c - длины сторон треугольника. Зная две из трех сторон или одну из сторон и угол, можно легко вычислить оставшуюся сторону.
3. Использование формулы синуса:
Если известны длины двух сторон треугольника и угол между ними, то можно использовать формулу синуса для вычисления третьей стороны. Формула выглядит следующим образом:
c = (a * sin(C)) / sin(A)
где a и c - длины известных сторон, A и C - углы треугольника, а c - длина третьей стороны.
Используя эти способы, можно определить стороны треугольника, имея достаточную информацию о его углах и длине сторон.
Вычисление косинуса треугольника через углы

Косинус треугольника с непрямым углом может быть вычислен через известные значения его углов. Для этого используется формула косинусов или теорема косинусов.
Формула косинусов гласит:
cos(A) = (b^2 + c^2 - a^2) / (2 * b * c)
где A - угол противоположный стороне a, b и c - стороны треугольника.
Способы вычисления косинуса треугольника через углы могут включать следующие шаги:
- Измерьте или определите значения всех углов треугольника.
- Выберите формулу косинусов для вычисления косинуса нужного угла.
- Подставьте известные значения сторон и угла в формулу и выполните необходимые вычисления.
Полученное значение косинуса может быть использовано в различных математических задачах или при вычислении других параметров треугольника, таких как длина сторон или площадь.
Как определить углы треугольника
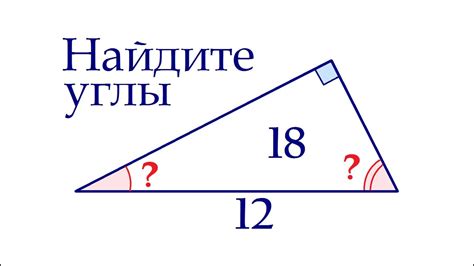
В треугольнике существует несколько методов для определения углов. Рассмотрим несколько из них:
1. Использование известных сторон треугольника
Если известны все три стороны треугольника, можно воспользоваться теоремой косинусов для определения углов. Формула выглядит следующим образом:
cos(A) = (b^2 + c^2 - a^2) / (2 * b * c)
Где A - угол между сторонами b и c, a, b, c - длины сторон треугольника.
2. Использование известных координат вершин треугольника
Если известны координаты вершин треугольника, можно воспользоваться геометрическими методами для определения углов. Например, можно использовать теорему синусов:
sin(A) = (b / a) = (c / d)
Где A - угол между сторонами a и b, a и b - стороны треугольника, c и d - длины отрезков, соединяющих вершины треугольника с какой-то точкой.
3. Использование свойств равнобедренного или прямоугольного треугольника
В равнобедренном треугольнике два угла равны между собой. В прямоугольном треугольнике один угол равен 90 градусам. Если треугольник имеет одно из этих свойств, можно определить углы без дополнительных расчетов.
Используя эти методы, можно определить углы треугольника и решать различные геометрические задачи.