Косинус угла между векторами - это один из важных понятий, которое часто используется в линейной алгебре, геометрии и физике. Он позволяет определить, насколько два вектора соотносятся друг с другом, и является мерой их схожести или ориентации друг относительно друга.
Один из способов вычисления косинуса угла между векторами - использование скалярного произведения. Векторное произведение представляет собой математическую операцию, результатом которой является число, называемое скалярным произведением. Оно равно произведению модулей векторов на косинус угла между ними.
Отличительной особенностью скалярного произведения является то, что оно позволяет не только получить числовое значение, но и определить ориентацию векторов - они будут сонаправленными, противонаправленными либо перпендикулярными друг другу, в зависимости от знака скалярного произведения.
Чтобы вычислить косинус угла между векторами с помощью скалярного произведения, необходимо найти значения скалярных произведений каждого вектора на самого себя и на другой вектор. Затем следует поделить скалярное произведение векторов на произведение их модулей.
Определение косинуса угла между векторами

Косинус угла между двумя векторами может быть найден с помощью скалярного произведения этих векторов. Косинус угла между векторами A и B обозначается как cos(θ).
Скалярное произведение векторов A и B вычисляется по формуле:
A · B = |A| · |B| · cos(θ)
где A и B - векторы, |A| и |B| - их длины.
Таким образом, для вычисления косинуса угла между векторами, можно воспользоваться следующей формулой:
cos(θ) = (A · B) / (|A| · |B|)
Значение косинуса угла между векторами может быть положительным или отрицательным, в зависимости от направлений векторов и их угла.
Косинус угла между векторами широко используется в различных областях науки, включая физику, математику, компьютерную графику, машинное обучение и др. Он позволяет определить сходство или различие между векторами и вычислять углы между ними.
Какая величина характеризует косинус угла между векторами?

Косинус угла между векторами вычисляется с использованием скалярного произведения этих векторов. Скалярное произведение двух векторов равно произведению их модулей на косинус угла между ними.
Значение косинуса угла между векторами находится в диапазоне от -1 до 1. Если косинус угла между векторами равен 1, это означает, что векторы сонаправлены и имеют одинаковое направление. Когда косинус угла равен 0, это говорит о том, что векторы ортогональны друг другу и не имеют общего направления. Если косинус угла равен -1, то векторы также сонаправлены, но они имеют противоположное направление.
Вычисление косинуса угла между векторами

Косинус угла между двумя векторами можно вычислить с помощью скалярного произведения этих векторов. Скалярное произведение векторов определяется как произведение их длин и косинуса угла между ними:
$$\veca} \cdot \vec\vec{b| \cdot \cos(\theta)$$
где $$\veca}$ и $\vec$ и $|$$ - их длины, $$\theta$$ - угол между ними.
Таким образом, чтобы найти косинус угла между векторами, необходимо разделить скалярное произведение этих векторов на произведение их длин:
$$\cos(\theta) = \frac\vec \cdot |}$$
Вычисление косинуса угла между векторами может быть полезно во многих областях, включая линейную алгебру, геометрию, физику и машинное обучение. Например, косинусное сходство между векторами может использоваться для определения степени схожести или различия между объектами.
Какое выражение позволяет найти косинус угла между векторами?

Косинус угла между двумя векторами может быть найден с помощью скалярного произведения векторов и их длин. Для этого используется следующее выражение:
| cos(θ) = | a · b | ─────────────── | ∥a∥ ∥b∥ |
где:
- cos(θ) - косинус угла между векторами a и b;
- a · b - скалярное произведение векторов a и b;
- ∥a∥ - длина вектора a;
- ∥b∥ - длина вектора b.
Используя это выражение, мы можем вычислить косинус угла между двумя векторами, зная значения их компонент. Полученное значение косинуса можно использовать для определения угла между векторами с помощью обратной функции cos(θ).
Использование скалярного произведения для нахождения косинуса угла
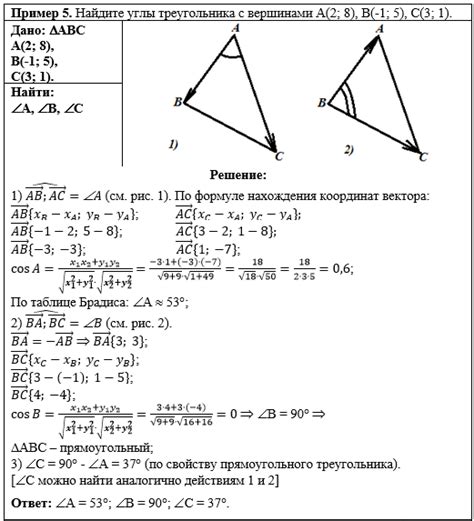
Для вычисления косинуса угла α между двумя векторами a и b, мы можем использовать следующую формулу:
cos(α) = (a · b) / (