Вычисление косинусов сторон треугольника может быть оказаться полезным во многих сферах, начиная от геометрии и заканчивая астрономией. Как правило, нахождение точного значения косинуса вручную является достаточно сложной задачей, поэтому используются различные приближенные формулы и методы.
Одним из самых распространенных методов вычисления косинусов сторон треугольника является формула косинусов. Согласно этой формуле, косинус угла треугольника равен отношению длины его противолежащей стороны к гипотенузе:
cos(α) = a / c
Где α - угол треугольника, a - длина противолежащей стороны, c - длина гипотенузы.
Для вычисления косинусов сторон треугольника можно использовать таблицы косинусов, которые содержат предварительно подсчитанные значения для различных углов. Также существуют специальные программы и онлайн-калькуляторы, которые позволяют получить точные значения косинусов сторон треугольника без необходимости проведения сложных вычислений вручную.
Зная косинусы сторон треугольника, можно решать различные задачи, связанные с его геометрическими свойствами, а также использовать эти значения в математических моделях и научных расчетах.
Вычисление косинусов сторон треугольника
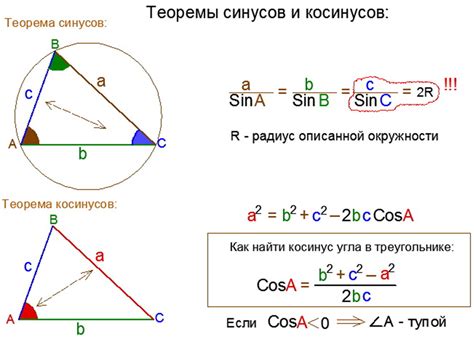
Косинусом стороны треугольника называется отношение длины этой стороны к длине гипотенузы прямоугольного треугольника, образованного этой стороной и двумя оставшимися сторонами.
Для вычисления косинуса стороны треугольника, сначала необходимо знать длины всех его сторон. После этого можно использовать формулу:
cos A = (b^2 + c^2 - a^2) / (2 * b * c)
cos B = (a^2 + c^2 - b^2) / (2 * a * c)
cos C = (a^2 + b^2 - c^2) / (2 * a * b)
Где:
- a, b, c - длины сторон треугольника
- A, B, C - углы, противолежащие сторонам a, b, c соответственно
Вычисление косинусов сторон треугольника может быть полезно в различных областях, таких как геометрия и тригонометрия. Например, зная косинусы сторон треугольника, можно рассчитать его площадь или найти другие углы.
Основные понятия и формулы

Косинус – это тригонометрическая функция, которая определяется как отношение прилежащего катета к гипотенузе прямоугольного треугольника.
Косинусы сторон треугольника – это значения косинусов углов, образуемых каждой из сторон треугольника с другими сторонами.
Существует несколько формул для вычисления косинусов сторон треугольника в зависимости от известных данных. Одна из таких формул – теорема косинусов:
Теорема косинусов:
В произвольном треугольнике со сторонами a, b и c и углом α против стороны a, углом β против стороны b и углом γ против стороны c, справедлива следующая формула:
a^2 = b^2 + c^2 - 2bc·cosα
b^2 = a^2 + c^2 - 2ac·cosβ
c^2 = a^2 + b^2 - 2ab·cosγ
При известных длинах сторон треугольника формулы теоремы косинусов позволяют вычислить косинусы углов.
Зная косинусы сторон треугольника, возможно вычислить другие характеристики треугольника, такие как площадь, радиусы вписанной и описанной окружностей, высоты и др.
Методика подбора точности вычислений

Для достижения высокой точности при вычислении косинусов сторон треугольника можно использовать следующую методику:
1. Определите требуемую точность, с которой необходимо вычислять косинусы. Например, точность до третьего знака после запятой.
2. Выберите алгоритм вычисления косинуса, который предлагает нужную точность. Существуют различные методы, такие как ряды Тейлора или интерполяция.
3. Разработайте программу, которая реализует выбранный алгоритм с нужной точностью. Учтите возможные ограничения и сложности вычислений, связанные с использованием повторных операций и хранением промежуточных результатов.
4. Проведите тестирование программы на различных значениях углов треугольника и сравните полученные результаты с точными значениями косинусов, вычисленными с использованием математических функций или специальных таблиц.
5. При необходимости проведите доработки программы или выберите другой алгоритм в зависимости от полученных результатов и требуемой точности.
6. Проверьте, что программа работает корректно для широкого диапазона значений углов треугольника и не вызывает ошибок округления или переполнения.
7. Запустите программу с требуемыми значениями углов и получите итоговые значения косинусов с нужной точностью.
8. Убедитесь, что полученные значения косинусов соответствуют ожидаемой точности и не требуют дополнительной корректировки.
При соблюдении данной методики и выборе подходящего алгоритма вы сможете вычислить косинусы сторон треугольника с необходимой точностью, учитывая специфику задачи и особенности вычислений.
Алгоритм расчета косинусов
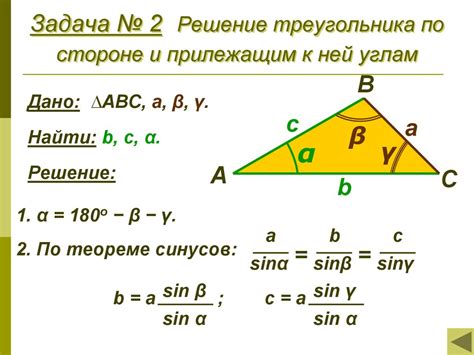
Для вычисления косинусов сторон треугольника с точностью можно использовать следующий алгоритм:
- Найдите длины всех сторон треугольника.
- Примените теорему косинусов для каждой стороны треугольника, используя следующую формулу:
cos(A) = (b^2 + c^2 - a^2) / (2 * b * c)
cos(B) = (a^2 + c^2 - b^2) / (2 * a * c)
cos(C) = (a^2 + b^2 - c^2) / (2 * a * b)
где A, B, C - углы треугольника, a, b, c - длины сторон треугольника. - Вычислите косинусы сторон треугольника, используя тригонометрическую функцию cos из стандартной библиотеки языка программирования, которым вы пользуетесь.
Таким образом, вы сможете вычислить косинусы сторон треугольника с заданной точностью. Этот алгоритм может быть полезен, например, при решении задач геометрии или вычисления треугольничных функций в программировании.
Использование тригонометрических таблиц
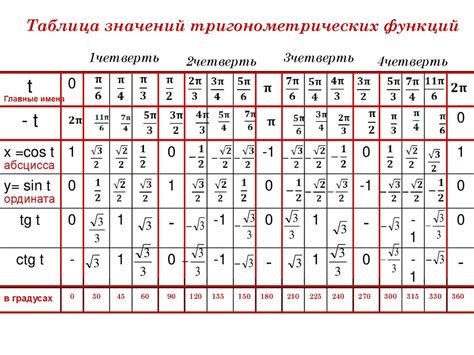
Для вычисления косинуса стороны треугольника, нужно знать значение угла этой стороны. После нахождения значения угла в таблице, можно найти соответствующее значение косинуса.
Прежде всего, необходимо определить, в каких единицах измеряется угол (радианы или градусы). Если угол измеряется в градусах, нужно найти соответствующую строку в таблице и найти значение косинуса в столбце с этим углом. Если угол измеряется в радианах, нужно выполнить преобразование из радиан в градусы и затем использовать таблицу.
Также можно использовать простой способ нахождения значений косинусов с помощью ломаной линии. Для этого на горизонтальной оси указываются значения углов, а на вертикальной оси - значения косинусов. Затем проводится ломаная линия, соединяющая точки с известными значениями косинусов. Для нахождения значения косинуса стороны треугольника, нужно найти значение угла на горизонтальной оси и прочитать соответствующее значение на вертикальной оси.
Использование тригонометрических таблиц является простым и эффективным способом вычисления косинусов сторон треугольника с точностью. Это позволяет избежать необходимости выполнения сложных математических операций и значительно ускоряет процесс вычислений.
Подготовка данных для вычислений

Для вычисления косинусов сторон треугольника с нужной точностью, необходимо иметь доступ к информации о значениях углов треугольника и длин сторон. В случае, если информация о сторонах треугольника уже известна, можно перейти непосредственно к вычислениям. В противном случае необходимо собрать и подготовить данные перед началом вычислений.
Важными данными для вычислений являются значения углов треугольника. Углы могут быть заданы в градусах или радианах. В случае, если углы уже заданы в нужном формате, данные можно использовать непосредственно. Если значения углов треугольника неизвестны, их можно вычислить с использованием известных данных о сторонах треугольника с помощью тригонометрических функций.
Начальные данные о сторонах треугольника могут быть представлены в виде длин отрезков либо соотношениями между сторонами (например, в виде отношения сторон в правильном треугольнике). Если длины сторон треугольника уже известны, данных можно использовать непосредственно. В противном случае необходимо их измерить или вычислить, воспользуясь доступными формулами или инструментами.
Также, перед вычислением косинусов сторон треугольника, полезно убедиться, что значения сторон и углов соответствуют принципам геометрии треугольника. Например, длины сторон треугольника должны быть положительными величинами, а сумма всех углов треугольника должна быть равна 180 градусов.
Перед началом вычислений необходимо также убедиться, что используемые формулы и методы вычисления косинусов сторон треугольника соответствуют требуемой точности. В зависимости от задачи, могут использоваться различные методы, включая численные алгоритмы или математические приближения. Важно выбрать подходящий метод, который обеспечит необходимую точность вычислений.
Влияние погрешностей на результаты
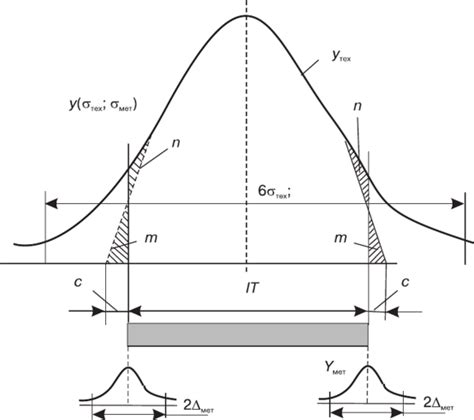
В процессе вычисления косинусов сторон треугольника с точностью могут возникать погрешности, которые могут заметно влиять на результаты. Погрешности могут возникать из-за неидеальности используемых математических моделей, неточности вычислений или неконтролируемых факторов.
Одной из наиболее распространенных погрешностей является округление чисел. При вычислениях косинусов сторон треугольника округление чисел может привести к накоплению погрешностей и результаты могут сильно отличаться от ожидаемых. Поэтому важно использовать высокоточные вычисления и минимизировать округление чисел, чтобы снизить влияние погрешностей.
Другим источником погрешностей является приближенная аппроксимация математических функций, таких как вычисление косинуса. В зависимости от используемого метода вычисления и точности, полученные результаты могут иметь небольшие отклонения от точных значений. Поэтому важно выбрать подходящий метод вычисления косинуса, который обеспечит требуемую точность.
Также следует учитывать, что погрешности могут возникать при вводе и обработке данных. Например, если входные данные содержат неточные и несовместимые значения, это может привести к некорректным результатам. Поэтому перед вычислением косинусов сторон треугольника важно проверить и предобработать входные данные, чтобы избежать возможных погрешностей.
В целом, для достижения наиболее точных результатов при вычислении косинусов сторон треугольника необходимо учесть все возможные источники погрешностей и принять соответствующие меры для их минимизации. Это можно сделать путем использования высокоточных вычислений, точных методов вычисления косинуса, проверки и предобработки данных, а также выбора подходящего округления результатов.
Применение теоремы косинусов
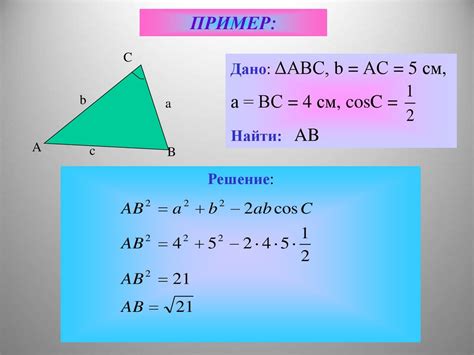
Формула теоремы косинусов выглядит следующим образом:
c^2 = a^2 + b^2 - 2ab * cos(C),
где c - длина стороны треугольника, a и b - длины двух других сторон, C - угол между этими сторонами.
Применение теоремы косинусов позволяет вычислить косинусы сторон треугольника, зная его размеры и углы. Это полезно для решения различных геометрических задач, например, для нахождения площади треугольника или определения его формы.
Теорема косинусов имеет широкое применение и может быть использована в различных областях, включая математику, физику, строительство и навигацию. Она является мощным инструментом для вычислений и анализа треугольников с точностью.
Решение задачи на вычисление косинуса стороны треугольника
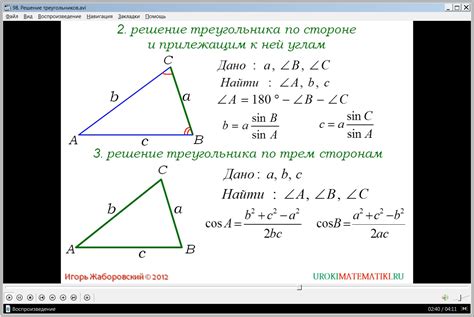
Для решения задачи по вычислению косинуса сторон треугольника с точностью, необходимо использовать известные значения двух других сторон треугольника и угла между ними.
Для начала, нужно определить известные значения. Допустим, у нас имеются стороны АВ и АС треугольника АВС, и известен угол между ними, равный α. Мы хотим вычислить косинус стороны ВС.
Для вычисления косинуса угла, можно использовать теорему косинусов:
| Теорема косинусов |
|---|
c² = a² + b² - 2ab · cos(α) |
Где:
- c – длина стороны, косинус которой требуется найти;
- a и b – известные стороны треугольника;
- α – известный угол между сторонами a и b.
Применяя теорему косинусов к нашей задаче, получим:
| Формула для косинуса стороны ВС: |
|---|
cos(α) = (a² + b² - c²) / (2ab) |
Таким образом, чтобы вычислить косинус стороны ВС треугольника АВС, нужно знать длины сторон АВ и АС, а также угол α между ними. Подставив соответствующие значения в формулу, получим результат.
Практические рекомендации для точного вычисления
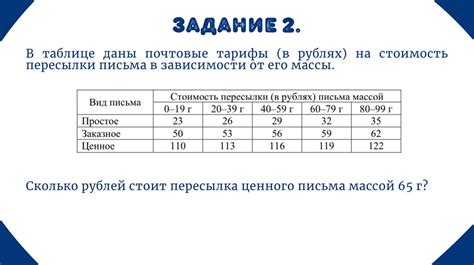
Вычисление косинусов сторон треугольника с высокой точностью может быть сложной задачей, однако, соблюдение некоторых рекомендаций может помочь в достижении желаемого результата:
1. Используйте точные значения углов:
Предварительно определите точные значения углов треугольника. Для этого можно воспользоваться тригонометрическими функциями, таблицами или формулами, соответствующими типу треугольника. Точные углы позволят получить более точные результаты.
2. Используйте точные значения сторон:
Для вычисления косинусов сторон треугольника с точностью необходимо знать точные значения длин этих сторон. Важно измерять стороны так, чтобы минимизировать погрешность. Для этого рекомендуется использовать точные инструменты измерения и проверять результаты несколько раз.
3. Используйте точные формулы:
Существует несколько формул для вычисления косинуса сторон треугольника с точностью. Некоторые из них, такие как теорема косинусов или правило синусов, могут использоваться для разных типов треугольников. Важно использовать формулы, соответствующие конкретному треугольнику, чтобы достичь максимальной точности.
4. Используйте точное программное обеспечение:
В некоторых случаях может быть полезно использовать специальное программное обеспечение для вычисления косинусов сторон треугольника с точностью. Такие программы могут предоставить более точные результаты за счет использования более сложных алгоритмов и расчетов. При выборе программного обеспечения обратите внимание на его надежность и точность вычислений.
Соблюдение вышеперечисленных рекомендаций поможет вам достичь более точных результатов при вычислении косинусов сторон треугольника. Однако следует помнить, что точность вычислений всегда ограничена сами значениями входных данных и методами их измерения.
Преимущества использования точных значений

Использование точных значений косинусов сторон треугольника имеет несколько преимуществ:
| 1. | Точные значения обеспечивают более высокую точность расчетов. Например, для построения графиков или проведения сложных математических операций, точные значения позволяют получить более точные результаты. |
| 2. | |
| 3. | Точные значения углов треугольника могут использоваться для решения задач геометрии, например, определения площадей или длин сторон треугольника. |
| 4. | При использовании точных значений косинусов сторон треугольника можно быть уверенным в их верности и надежности. Это особенно важно при выполнении сложных математических операций, где допущение даже небольшой погрешности может привести к неверному результату. |
В целом, использование точных значений косинусов сторон треугольника позволяет получить более точные результаты в анализе и расчетах, а также обеспечивает надежность и верность полученных данных.