Тангенс и котангенс - это две взаимосвязанные тригонометрические функции, которые часто используются в математике и физике. Тангенс определяется как отношение противоположной стороны катета к прилежащей стороне, а котангенс - как обратное значение тангенса. Расчет котангенса по тангенсу может быть полезным при решении различных задач и задач, связанных с геометрией и тригонометрией.
Для расчета котангенса по заданному значению тангенса необходимо знать несколько простых правил. Во-первых, котангенс - это обратное значение тангенса, поэтому чтобы найти котангенс, нужно найти обратное значение тангенса и умножить его на -1. Во-вторых, тангенс и котангенс являются функциями, период которых равен 180 градусам или \(\pi\) радианам. Поэтому для нахождения котангенса по тангенсу необходимо определить, находится ли заданное значение тангенса в первом, втором, третьем или четвертом квадрантах.
Найденный котангенс может быть использован для решения различных задач, включая вычисление углов, определение длин и площадей, нахождение коэффициентов пропорциональности и многое другое. Знание правил и методов расчета котангенса по тангенсу позволит вам более точно и оперативно решать задачи, связанные с тригонометрией, и повысить уровень своих математических навыков.
Что такое тангенс и котангенс:
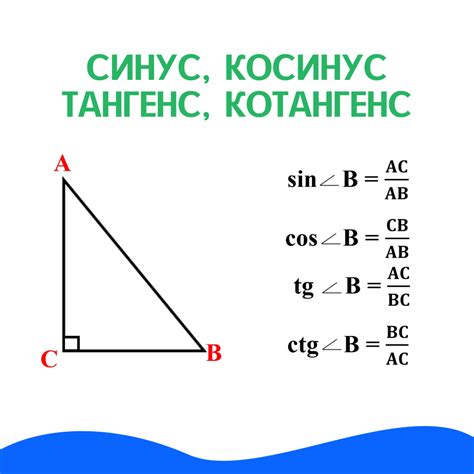
Тангенс (tg) определяется как отношение противолежащего катета к прилежащему катету в прямоугольном треугольнике.
Котангенс (ctg) - это обратная функция тангенсу и определяется как отношение прилежащего катета к противолежащему катету в прямоугольном треугольнике.
Для вычисления тангенса или котангенса необходимо знать значения противолежащего и прилежащего катетов в треугольнике, а затем применить соответствующую формулу.
Тангенс и котангенс широко применяются в геометрии, физике и других областях науки и техники.
Определение и основные свойства

Котангенсом угла α называется отношение смежного катета к противолежащему катету в прямоугольном треугольнике.
Формула для расчета котангенса выглядит следующим образом:
cot(α) = cos(α)/sin(α)
Основное свойство котангенса заключается в том, что он является обратным значением тангенса:
cot(α) = 1/tan(α)
Котангенс также обладает следующими свойствами:
- Котангенс отрицательного угла α равен отрицательному котангенсу угла α:
- Котангенс комплементарных углов α и (90° - α) равен квадратному корню из отношения смежного катета к противолежащему:
- Котангенс смежных углов α и (α + 180°) равен минус единице:
- Котангенс определен только для ненулевых углов, так как в прямоугольном треугольнике противолежащий катет не может быть равен нулю.
cot(-α) = -cot(α)
cot(α) = sqrt(cot(90° - α))
cot(α) = -1
При расчете котангенса необходимо обращать внимание на правильную интерпретацию результатов и учитывать данные ограничения.
Как найти тангенс по углу:
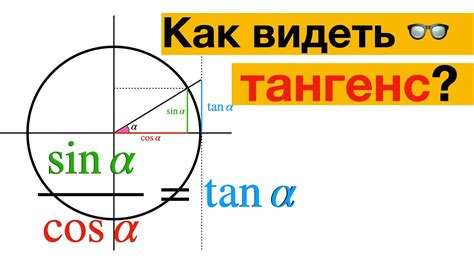
Для нахождения тангенса по углу необходимо разделить значения противолежащего катета и прилежащего катета прямоугольного треугольника.
Формула для расчета тангенса угла будет выглядеть следующим образом:
тангенс угла = противолежащий катет / прилежащий катет
Для примера, если противолежащий катет равен 4, а прилежащий катет равен 3, тогда:
тангенс угла = 4 / 3 = 1.3333
Таким образом, тангенс угла равен 1.3333.
Формула и примеры расчета

Для расчета котангенса по тангенсу используется следующая формула:
котангенс α = 1 / тангенс α
Продемонстрируем это на примере:
Допустим, у нас есть значение тангенса α, равное 0,75. Чтобы найти котангенс α, мы можем применить формулу:
котангенс α = 1 / 0,75 = 1,3333
Таким образом, котангенс α равен 1,3333.
Как найти котангенс по углу:
Чтобы найти котангенс (ℙ) по заданному углу (α), нужно выполнить следующие шаги:
Шаг 1: Найдите тангенс (ℓ) по заданному углу (α) с помощью расчетной формулы ℓ = sin(α) / cos(α).
Шаг 2: Используйте полученное значение тангенса (ℓ) для расчета котангенса (ℙ) по формуле ℙ = 1 / ℓ.
Пример:
Допустим, задан угол α = 45°.
Шаг 1: Найдем тангенс (ℓ) по формуле ℓ = sin(α) / cos(α). Подставляя значения, получаем:
ℓ = sin(45°) / cos(45°) = 1 / 1 = 1.
Шаг 2: Используя найденное значение тангенса (ℓ), найдем котангенс (ℙ) по формуле ℙ = 1 / ℓ. Подставляя полученное значение, получаем:
ℙ = 1 / 1 = 1.
Таким образом, котангенс угла 45° равен 1.
Соотношение с тангенсом и примеры расчета
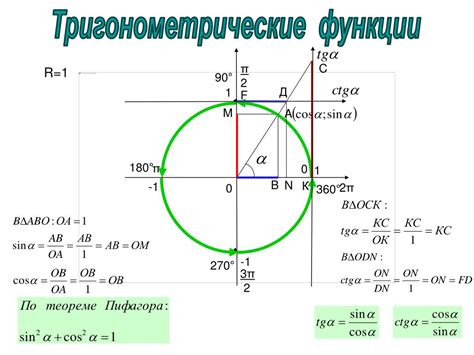
cot(θ) = 1 / tan(θ)
Для расчета котангенса по известному значению тангенса необходимо взять обратное значение тангенса и применить к нему операцию деления на 1. Например, если тангенс угла θ равен 0,577, то:
cot(θ) = 1 / tan(θ) = 1 / 0,577 = 1,732
Таким образом, котангенс угла θ равен 1,732.
Еще один пример: если тангенс угла θ равен -0,75, то:
cot(θ) = 1 / tan(θ) = 1 / (-0,75) = -1,333
Таким образом, котангенс угла θ равен -1,333.
Такие простые правила и методы позволяют легко находить котангенс по известному значению тангенса и обратно.
Методы расчета котангенса по тангенсу:
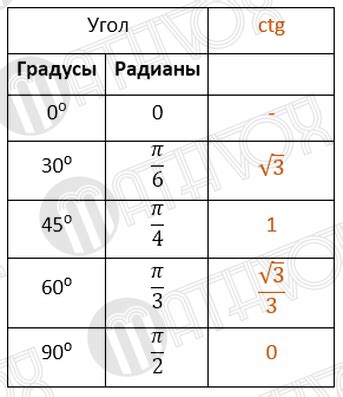
Для нахождения котангенса по тангенсу можно использовать несколько методов:
1. Математическая формула:
Котангенс (ctg) выражается как обратная величина тангенса (tg):
ctg(x) = 1/tg(x)
2. Связь котангенса с синусом и косинусом:
Котангенс может быть выражен через соотношение между синусом (sin) и косинусом (cos):
ctg(x) = cos(x)/sin(x)
3. Использование таблиц или калькуляторов:
Если точное значение котангенса не требуется, можно воспользоваться таблицей значений тригонометрических функций или электронным калькулятором, где котангенс уже рассчитан для различных углов.
Выбор метода зависит от задачи и доступности необходимой информации. Знание различных методов расчета котангенса по тангенсу может быть полезно при решении разнообразных задач в математике и естественных науках.
Алгоритмы и примеры использования
Алгоритм расчета котангенса по тангенсу:
1. Задать значение тангенса.
2. Рассчитать значение соседнего катета по формуле катета: c = 1 / тангенс.
3. Рассчитать гипотенузу по формуле гипотенузы: гипотенуза = sqrt(катет^2 + c^2).
4. Рассчитать значение котангенса по формуле котангенса: котангенс = c / гипотенуза.
5. Полученное значение котангенса является результатом расчета.
Пример использования:
Пусть тангенс угла равен 0.6.
Рассчитаем котангенс:
1. c = 1 / 0.6 = 1.6667
2. гипотенуза = sqrt((0.6)^2 + (1.6667)^2) = 1.807
3. котангенс = 1.6667 / 1.807 = 0.92
Таким образом, котангенс угла с тангенсом 0.6 равен 0.92.
Почему важно знать тангенс и котангенс:
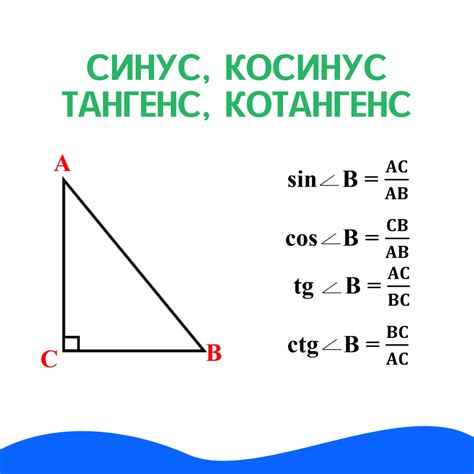
Тангенс угла представляет отношение противоположной стороны к прилежащей стороне прямоугольного треугольника. Это позволяет определить угол, зная длины сторон. Котангенс, в свою очередь, является обратной функцией тангенсу и определяется как отношение прилежащей стороны к противоположной. Оба этих понятия необходимы для решения задач, связанных с треугольниками и геометрией.
Однако знание тангенса и котангенса полезно не только в геометрии. Оно также играет важную роль в физике, астрономии и инженерии. Например, в механике тангенс используется для определения угла наклона трактора или неглубоких склонов, а в электротехнике и астрономии он позволяет определить угол падения света на поверхность и другие параметры.
Знание тангенса и котангенса дает возможность более точно измерять и предсказывать различные явления при работе с углами и треугольниками. Оно также позволяет лучше понимать и анализировать различные физические и геометрические процессы. Поэтому важно освоить расчеты тангенса и котангенса и использовать их при решении задач и проведении измерений в соответствующих областях науки и техники.