Многогранники с прямыми двугранными углами - это геометрические фигуры, в которых все углы между гранями являются прямыми. Такие многогранники имеют много интересных свойств и широко используются в различных областях, включая архитектуру, науку и искусство. Однако вычисление объема таких многогранников может быть задачей, достаточно сложной для понимания.
В этой статье мы предоставим вам пошаговое руководство по нахождению объема многогранника с прямыми двугранными углами. Мы рассмотрим основные формулы и примеры, которые помогут вам лучше понять эту тему и применить полученные знания на практике.
Прежде чем начать вычисления, необходимо понять основные понятия, связанные с многогранниками с прямыми двугранными углами. Эти фигуры состоят из плоских граней, которые могут быть различных форм и размеров. Каждая грань имеет свою площадь и высоту, которые будут использоваться при нахождении объема многогранника.
Формула для вычисления объема многогранника с прямыми двугранными углами зависит от конкретной формы многогранника, поэтому для каждого типа многогранника может быть своя формула. Например, для прямоугольного параллелепипеда объем можно вычислить умножением длины, ширины и высоты. Однако, для более сложных многогранников, таких как призмы, пирамиды или додекаэдры, формулы могут быть более сложными и требовать дополнительных вычислений.
Как найти объем многогранника
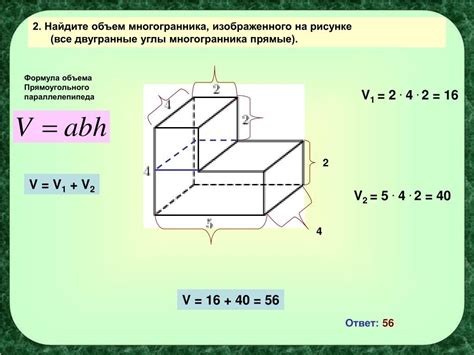
Существует несколько формул для определения объема многогранника в зависимости от его формы и свойств.
Вот несколько формул для рассчета объема многогранника в зависимости от его формы:
| Форма многогранника | Формула |
|---|---|
| Параллелепипед | V = a * b * h |
| Куб | V = a * a * a |
| Призма | V = b * h |
| Пирамида | V = (1/3) * b * h |
| Цилиндр | V = π * r^2 * h |
Для многогранников с более сложной формой, таких как икосаэдр или додекаэдр, формулы для рассчета объема могут быть более сложными и требуют дополнительных параметров.
Важно знать, что размеры многогранника должны быть выражены в одной и той же единице измерения, чтобы рассчитать объем корректно.
Теперь, зная основные формулы для определения объема многогранника, вы можете эффективно решать задачи, связанные с геометрией и пространственными фигурами.
Прямые двугранные углы: руководство и формулы
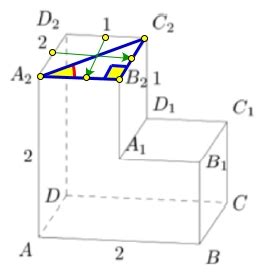
Прямой двугранный угол - это угол между двумя плоскостями, которые пересекаются под прямым углом. Он образуется двумя прямыми, пересекающимися в точке исходного угла.
Чтобы вычислить объем многогранника с прямыми двугранными углами, необходимо знать длину каждой стороны многогранника и прямые двугранные углы. Существует несколько формул, которые могут быть использованы для вычисления объема в зависимости от типа многогранника.
| Многогранник | Формула для вычисления объема |
|---|---|
| Параллелепипед | Объем = длина * ширина * высота |
| Пирамида | Объем = (площадь основания * высота) / 3 |
| Призма | Объем = площадь основания * высота |
| Цилиндр | Объем = площадь основания * высота |
Например, если у нас есть параллелепипед с длиной 5, шириной 3 и высотой 2, мы можем вычислить его объем, умножив все три измерения в соответствии с формулой:
Объем = 5 * 3 * 2 = 30
Таким образом, объем этого параллелепипеда равен 30.
Использование прямых двугранных углов позволяет нам более точно и эффективно вычислять объемы многогранников. Изучение приведенных формул поможет вам использовать этот метод при решении различных геометрических задач.