Как вычислить объем пирамиды, образованной правильным четырехугольником?

Правильные четырехугольники - это особый класс геометрических фигур, имеющих четыре равных стороны и четыре равных угла. Они представляют собой идеальную основу для построения пирамиды. Ведь пирамида - это трехмерная фигура, основанием которой служит плоскость, а бока - треугольные грани, сходящиеся в одной вершине.

Однако, чтобы найти объем такой пирамиды, нам понадобится знать не только размеры основания, но и высоту. Высота пирамиды - это расстояние от вершины до плоскости основания. Кроме того, обратим внимание, что для нахождения объема пирамиды необходимо знать площадь основания, а не периметр.

Стоит отметить, что для правильного четырехугольника формулу нахождения площади основания можно упростить. Достаточно перемножить длины двух диагоналей и результат разделить на 2. Таким образом, площадь основания будет равна половине произведения длин диагоналей.

Определение правильного четырехугольника

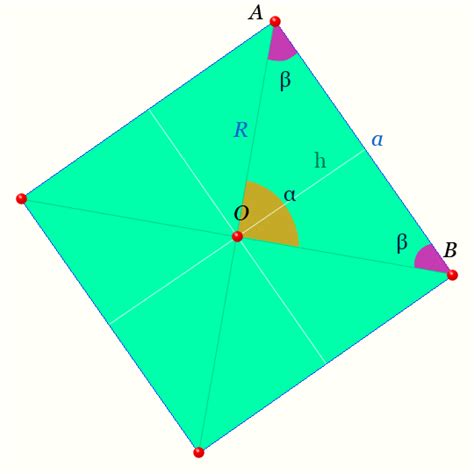
Существуют несколько способов определения правильного четырехугольника:

• Геометрическое определение: Есть несколько определений, которые можно использовать, чтобы классифицировать четырехугольник как правильный. Одно из них - это сказать, что углы четырехугольника равны 90 градусам, а соседние стороны равны.
• Алгебраическое определение: Еще один способ определения правильного четырехугольника - использование алгебраических свойств. Если все углы и стороны четырехугольника равны, то его можно классифицировать как правильный.

Правильный четырехугольник является простой и симметричной фигурой, которая имеет много применений в геометрии и науке, включая построение пирамиды.

Понятие правильного четырехугольника и его особенности

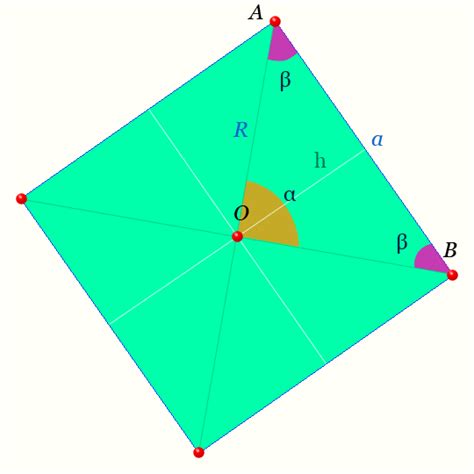
Изучение правильного четырехугольника позволяет нам понять его особенности и свойства. Вот некоторые из них:

• Все стороны правильного четырехугольника равны;
• Все углы правильного четырехугольника равны и составляют 90 градусов;
• Диагонали правильного четырехугольника равны;
• Площадь правильного четырехугольника можно вычислить, зная длину стороны;
• Периметр правильного четырехугольника можно вычислить, умножив длину стороны на 4.

Правильный четырехугольник играет важную роль в геометрии и имеет множество применений в повседневной жизни, а также в различных научных и инженерных областях.

Изучение правильных четырехугольников является важным шагом в изучении более сложных геометрических объектов и конструкций, таких как пирамиды и другие трехмерные фигуры.

Вычисление площади правильного четырехугольника

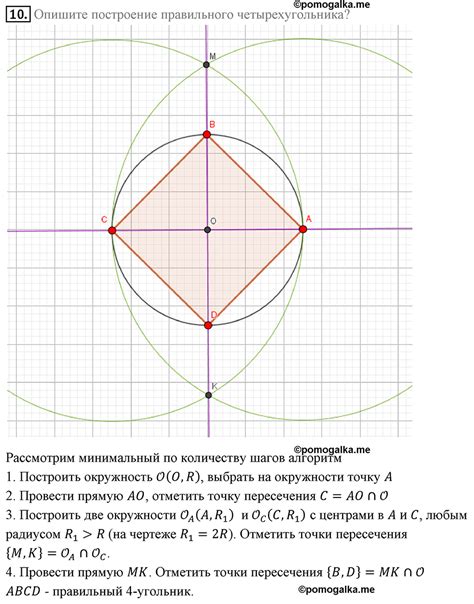
Площадь правильного четырехугольника можно вычислить, используя формулу, основанную на длинах его сторон и диагоналей. В случае, если все стороны равны между собой и все углы прямые, прямоугольника можно считать правильным.

Для вычисления площади прямоугольника нужно умножить длину одной из его сторон на длину другой стороны: S = a * b, где a и b - длины сторон прямоугольника.

Если известны длины обеих диагоналей прямоугольника, то площадь можно вычислить по формуле: S = (d₁ * d₂) / 2, где d₁ и d₂ - длины диагоналей прямоугольника.

Если известна длина стороны прямоугольника и его длина диагонали, то площадь можно вычислить по формуле: S = (a * d) / 2, где a - длина стороны прямоугольника, d - длина диагонали прямоугольника.

Важно помнить, что все значения должны быть выражены в одной единице измерения, иначе результат будет некорректным. Также необходимо учесть единицы измерения при записи ответа.

Формула для вычисления площади правильного четырехугольника

Площадь = (a * h) / 2

Где:

• a - длина стороны четырехугольника
• h - длина высоты четырехугольника

Следует помнить, что длина высоты падает перпендикулярно к основанию четырехугольника и проходит через его вершину.

Построение пирамиды на основе правильного четырехугольника

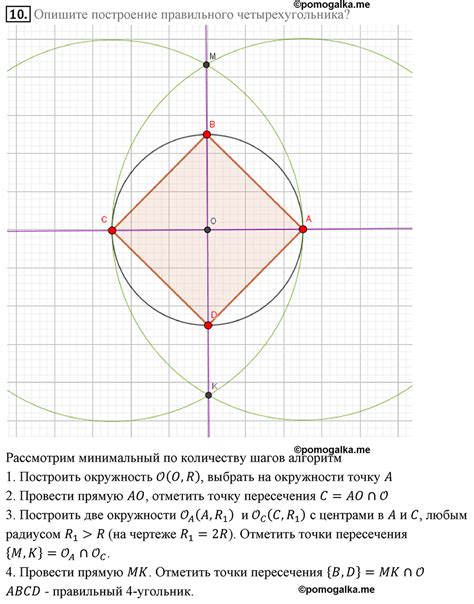
Для начала нам необходимо найти значение длины стороны правильного четырехугольника. Это можно сделать с помощью формулы:

a = h / √2

где a - длина стороны правильного четырехугольника, h - высота пирамиды.

Зная значение длины стороны, мы можем вычислить площадь основания пирамиды с помощью формулы:

S = a^2

Теперь, когда у нас есть площадь основания, нам нужно найти высоту пирамиды. Если высота пирамиды равномерно распределена по высоте правильного четырехугольника, то высота пирамиды равна высоте правильного четырехугольника.

И, наконец, используя значение площади основания и высоты пирамиды, мы можем вычислить объем пирамиды по формуле:

V = (S * h) / 3

Теперь у нас есть все необходимые инструкции для построения пирамиды на основе правильного четырехугольника. Не забудьте проверить вычисления и обратиться к дополнительным источникам, если вам понадобится дополнительная информация. Успехов в строительстве!

Как построить пирамиду на основе правильного четырехугольника

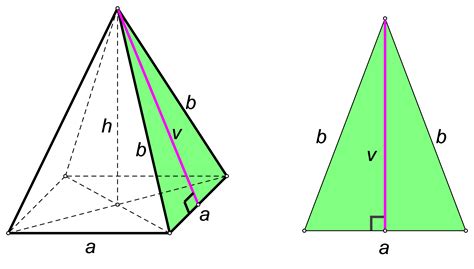
1. Нарисуйте правильный четырехугольник. Это должен быть четырехугольник, у которого все стороны и углы равны между собой. Каждый угол в нем должен быть равным 90 градусам, а его стороны должны быть равными.
2. Установите одну из сторон четырехугольника горизонтально на плоскости. Она будет служить основанием пирамиды.
3. Отметьте середину основания и прямоугольника. Отметьте также вершины, находящиеся противоположно друг другу.
4. Соедините вершины пирамиды с серединой основания. Эти отрезки будут боковыми ребрами пирамиды.
5. Высоту пирамиды можно найти, используя теорему Пифагора. Для этого измерьте длину стороны пирамиды и расстояние от середины основания до вершины пирамиды. Примените теорему Пифагора: квадрат длины стороны плюс квадрат расстояния до вершины равно квадрату высоты. Найдите квадратный корень от этой суммы, чтобы найти высоту.

Теперь, следуя этим шагам, вы сможете построить пирамиду на основе правильного четырехугольника. Такая пирамида будет иметь основание с четырьмя равными сторонами и четырьмя прямыми углами.

Нахождение объема пирамиды из правильного четырехугольника

Используя формулу для объема пирамиды, можно вычислить его значение: V = (S основания * h) / 3, где V - объем пирамиды, S основания - площадь основания, h - высота пирамиды.

Для нахождения площади основания правильного четырехугольника, можно воспользоваться формулой: S = a^2, где a - длина одной из сторон основания.

После нахождения площади основания и зная высоту пирамиды, подставляем значения в формулу для объема пирамиды и получаем окончательный результат.

Таким образом, нахождение объема пирамиды из правильного четырехугольника сводится к вычислению площади основания и использованию формулы для объема пирамиды.