Объем прямой призмы цилиндра является одним из основных понятий в геометрии, которое школьникам предстоит изучать в рамках курса математики. Практическое применение данной темы очень широко – оно находит свое применение в строительстве, инженерии и архитектуре.
Понимание концепции объема прямой призмы цилиндра поможет школьнику лучше освоить этот материал и успешнее справиться с проверками и домашними заданиями. В данной статье мы рассмотрим, как найти объем прямой призмы цилиндра с использованием простых и понятных формул.
Цилиндр – это геометрическое тело, имеющее два равных и параллельных круглая основания, соединенных боковой поверхностью, которая является цилиндрической поверхностью. Призма же - это геометрическое тело, у которого база состоит из двух несовпадающих оснований, параллельных между собой. Таким образом, прямая призма цилиндра является объединением этих двух геометрических фигур.
Объем прямой призмы цилиндра определяется как объем цилиндра, помноженный на высоту призмы. Для нахождения объема необходимо знать радиус основания цилиндра (r) и высоту основания (h). Формула для нахождения объема прямой призмы цилиндра имеет вид: V = π * r^2 * h.
Что такое объем прямой призмы цилиндра?

Для вычисления объема прямой призмы цилиндра необходимо знать высоту цилиндра и площадь его основания. Объем прямой призмы цилиндра вычисляется по формуле:
V = S * h
где V - объем цилиндра, S - площадь основания цилиндра, h - высота цилиндра.
Объем прямой призмы цилиндра измеряется в кубических единицах объема, например, в кубических метрах (м³) или кубических сантиметрах (см³).
Как вычислить объем прямой призмы цилиндра?

Объем прямой призмы цилиндра можно вычислить с помощью следующей формулы:
Объем = площадь основания × высота
Чтобы рассчитать объем прямой призмы цилиндра, нужно знать площадь основания и высоту. Площадь основания для цилиндра равна площади круга, что можно выразить по формуле:
Площадь основания = π × радиус^2
Высота цилиндра - это расстояние между основаниями. Если оба основания одинаковы и находятся на одном уровне, то высота равна расстоянию между ними.
Итак, чтобы найти объем прямой призмы цилиндра, нужно сначала найти площадь основания, а затем умножить ее на высоту цилиндра.
Например, предположим, что радиус основания цилиндра равен 4 см, а высота равна 10 см. Для начала найдем площадь основания:
Площадь основания = π × 4^2 = 16π см^2
Теперь, умножим площадь основания на высоту, чтобы найти объем:
Объем = 16π см^2 × 10 см = 160π см^3
Таким образом, объем этого цилиндра равен 160π см^3.
Теперь вы знаете, как вычислить объем прямой призмы цилиндра. Удачного расчета!
Как найти площадь основания прямой призмы цилиндра?

Площадь основания прямой призмы цилиндра можно найти, зная форму основания и его размеры.
Если основание прямой призмы цилиндра является кругом, то его площадь можно найти по формуле:
Площадь основания = π * радиус^2
где π (пи) - математическая константа, примерное значение которой равно 3,14, а радиус - расстояние от центра основания до любой точки его окружности. Площадь основания прямой призмы цилиндра будет выражена в квадратных единицах (например, квадратных сантиметрах или квадратных метрах).
Если основание прямой призмы цилиндра имеет форму многоугольника, то его площадь можно найти, разбив его на более простые фигуры и вычислив площади каждой из них. Например, если основание является правильным n-угольником, то его площадь можно найти по формуле:
(Площадь основания) = (1/4) * n * сторона2 * cot(π/n)
где n - количество сторон многоугольника, сторона - длина одной стороны многоугольника, cot - тригонометрическая функция котангенс.
Таким образом, для нахождения площади основания прямой призмы цилиндра необходимо знать форму основания (круг, многоугольник) и его размеры (радиус, количество сторон и длины сторон).
Формула для вычисления объема прямой призмы цилиндра
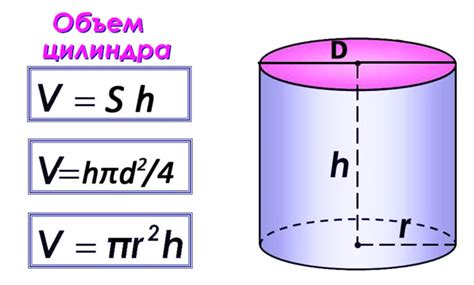
Объем прямой призмы цилиндра может быть вычислен с использованием следующей формулы:
- Измерьте высоту цилиндра (h) в любых единицах, например в сантиметрах.
- Измерьте радиус основания цилиндра (r) в тех же единицах.
- Воспользуйтесь формулой для вычисления объема прямой призмы цилиндра: Объем = π * r^2 * h.
Здесь π (пи) - математическая константа, приближенное значение которой равно приблизительно 3,14159.
Однако, если значение π в вашей формуле неизвестно или не важно, вы можете использовать приближенное значение 3,14 для расчета.
Убедитесь, что ваши измерения основаны на одной и той же единице измерения, иначе результат может быть некорректным.
Примеры решения задач на вычисление объема прямой призмы цилиндра

Для решения задач на вычисление объема прямой призмы цилиндра, необходимо знать формулу для расчета объема. Объем цилиндра можно вычислить, используя формулу:
V = S * h,
где V - объем цилиндра, S - площадь основания цилиндра, h - высота цилиндра.
Рассмотрим несколько примеров:
Пример 1:
Найдем объем прямой призмы цилиндра, если площадь основания равна 25 квадратных сантиметров, а высота равна 10 сантиметров.
Подставим значения в формулу:
V = 25 * 10 = 250 сантиметров кубических.
Ответ: объем прямой призмы цилиндра равен 250 сантиметров кубических.
Пример 2:
Найдем объем прямой призмы цилиндра, если площадь основания равна 50 квадратных сантиметров, а высота равна 8 сантиметров.
Подставим значения в формулу:
V = 50 * 8 = 400 сантиметров кубических.
Ответ: объем прямой призмы цилиндра равен 400 сантиметров кубических.
Таким образом, для решения задач на вычисление объема прямой призмы цилиндра необходимо знать площадь основания и высоту цилиндра, а затем подставить их в формулу для расчета объема. Это позволит найти объем цилиндра и дать точный ответ на поставленную задачу.
Важные особенности при вычислении объема прямой призмы цилиндра
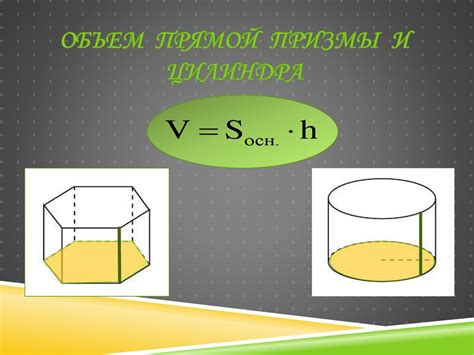
1. Формула для вычисления объема: Для прямой призмы цилиндра формула для вычисления объема имеет вид V = S * h, где V - объем, S - площадь основания, h - высота. В данном случае S будет равно площади основания цилиндра, а h - высоте призмы.
2. Единицы измерения: При вычислении объема прямой призмы цилиндра важно используемые единицы измерения. Чтобы получить правильный результат, необходимо убедиться, что все измерения проводятся в одной системе - метрической или английской. Также важно правильно указывать единицы измерения при записи ответа.
3. Правильное измерение: Чтобы вычисления были точными, необходимо правильно измерить все параметры, необходимые для нахождения объема. В случае прямой призмы цилиндра это площадь основания и высота. При измерении площади основания, следует учесть форму фигуры (обычно это круг) и правильно измерить радиус или диаметр. Высота призмы также должна быть измерена точно.
4. Зависимость объема от высоты: Объем прямой призмы цилиндра пропорционален её высоте. Это означает, что если высоту удвоить, объем также удвоится. Таким образом, изменение высоты прямой призмы цилиндра может значительно влиять на объем. Знание этой особенности может помочь в решении задач, где необходимо сравнивать объемы призм с разными высотами.
Учитывание этих важных особенностей позволит вам правильно решать задачи, связанные с вычислением объема прямой призмы цилиндра. Не забывайте учиться и проводить измерения с максимальной точностью, чтобы получить правильные результаты.