Шестиугольная наклонная призма - геометрическое тело, имеющее шесть граней, из которых три являются наклонными и три - основаниями. Это особый вид призмы, который привлекает внимание своей необычной формой и сложностью расчетов. Однако, с помощью определенных формул и правил, можно легко определить ее объем.
Первым шагом для расчета объема шестиугольной наклонной призмы необходимо найти площадь одного из оснований. Для шестиугольника площадь вычисляется по формуле: площадь = (3 * √3 * a^2) / 2, где "a" - длина стороны шестиугольника. Полученное значение площади основания поможет нам далее в расчете объема.
Далее, для определения объема шестиугольной наклонной призмы необходимо найти высоту. Высоту можно найти, используя формулу: высота = объем / площадь основания. Объем наклонной призмы определяется по формуле: объем = площадь основания * высота.
Итак, для того чтобы рассчитать объем шестиугольной наклонной призмы, необходимо последовательно выполнить несколько шагов: найти площадь одного из оснований по формуле, вычислить высоту по объему и площади основания, а затем найти объем призмы по формуле. В результате получим точное значение объема данного геометрического тела.
Какие формулы использовать для расчета объема шестиугольной наклонной призмы?

Для расчета объема шестиугольной наклонной призмы можно использовать следующие формулы:
- Длина боковой грани призмы: a.
- Площадь основания призмы: S.
Формула для расчета объема шестиугольной наклонной призмы:
V = 3Sа, где V - объем призмы, S - площадь основания, а - длина боковой грани.
Чтобы рассчитать объем шестиугольной наклонной призмы, необходимо знать длину боковой грани и площадь основания. Длина боковой грани обозначается как a, а площадь основания - как S. Подставив значения в формулу, можно получить объем призмы.
Описание формы призмы
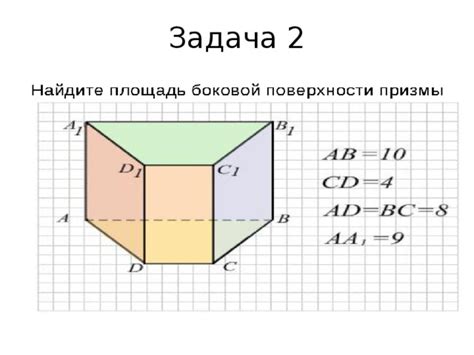
Основанием шестиугольной наклонной призмы является шестиугольник, имеющий шесть одинаковых сторон и шесть равных углов. Все боковые грани имеют форму трапеции, с одним параллельным основанием и одной общей стороной соседних трапеций.
У шестиугольной наклонной призмы есть три пары параллельных ребер: шесть боковых ребер, соединяющих боковые грани, и шесть основных ребер, соединяющих вершины оснований.
Для определения объема шестиугольной наклонной призмы необходимо знать длину основания и высоту призмы. Площадь основания призмы вычисляется как произведение длины одной стороны шестиугольника на высоту призмы.
| Формула для расчета объема шестиугольной наклонной призмы: |
|---|
| V = S * h |
Где:
- V - объем призмы
- S - площадь основания призмы
- h - высота призмы
Расчет площади основания призмы
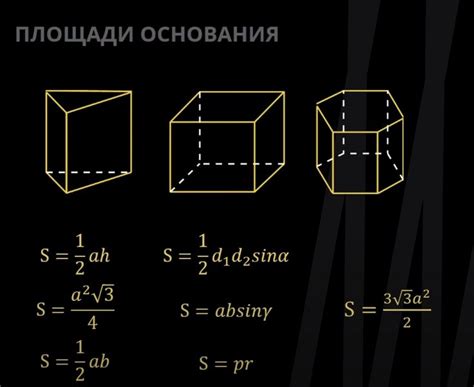
Для расчета объема шестиугольной наклонной призмы необходимо знать площадь ее основания. Площадь основания призмы определяется формулой, зависящей от вида фигуры основания.
Если основание призмы является шестиугольником, то площадь его можно найти следующим образом:
| Вид основания | Формула для расчета площади |
|---|---|
| Равносторонний шестиугольник | S = (3 * a2 * √3) / 2 |
| Произвольный шестиугольник | S = (3 * a1 * a2 * sin(π/3)) |
Где:
- S - площадь основания призмы;
- a - длина стороны равностороннего шестиугольника;
- a1, a2 - длины двух сторон произвольного шестиугольника.
Выберите формулу в зависимости от вида фигуры основания и подставьте известные значения в формулу для определения площади основания призмы.
Как найти высоту призмы?
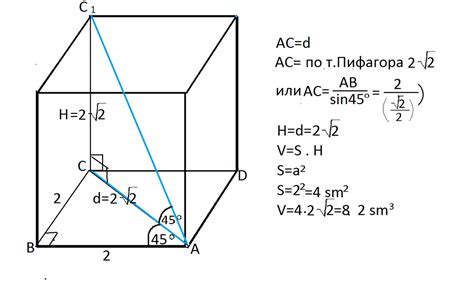
Существует несколько способов найти высоту призмы, в зависимости от доступных данных:
1. Высота призмы через объем:
Если известен объем призмы и площадь одной из ее основ, высоту можно найти с помощью формулы:
высота = объем / площадь основы
2. Высота призмы через площадь основы и боковую площадь:
Если известны площадь одной из основ и боковая площадь призмы, можно использовать формулу:
высота = (2 * площадь основы) / боковая площадь
3. Высота призмы через длину ребра и площадь основы:
Если известны длина ребра и площадь одной из основ, можно найти высоту с помощью формулы:
высота = площадь основы / (корень из 3 * длина ребра)
Пользуясь этими формулами, можно рассчитать высоту шестиугольной наклонной призмы, зная соответствующие данные. Убедитесь, что все единицы измерения согласованы, чтобы получить правильный результат.