Шестиугольная призма является одним из наиболее интересных и сложных геометрических объектов. Однако, в отличие от многих других фигур, вычисление объема шестиугольной призмы является достаточно простой операцией, особенно если используется ребро в качестве известного параметра.
Объем шестиугольной призмы может быть вычислен при помощи формулы, которая основана на ее высоте и площади основания. Однако, для расчета объема по ребру также необходимо знать еще один параметр - длину сторон основания. Что делать в случае, если эта информация недоступна?
Оказывается, что можно найти объем шестиугольной призмы только зная длину ее одного ребра! Для этого можно воспользоваться следующей формулой: V = (3 * √3 * a^2 * h) / 2, где V - объем, a - длина ребра, h - высота.
Определение шестиугольной призмы
Формула для вычисления объема
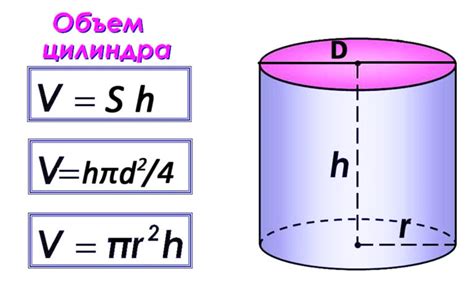
Для вычисления объема шестиугольной призмы, вам понадобится знать длину ребра и высоту призмы. Формула для вычисления объема шестиугольной призмы выглядит следующим образом:
| Обозначение | Описание |
|---|---|
| V | Объем шестиугольной призмы |
| a | Длина ребра призмы |
| h | Высота призмы |
Формула для вычисления объема шестиугольной призмы выглядит следующим образом:
V = 3 * sqrt(3) * a^2 * h
Где:
- 3 - число корней кубического корня из 3;
- sqrt(3) - квадратный корень из 3;
- a - длина ребра призмы;
- h - высота призмы.
Используя эту формулу, вы можете легко вычислить объем шестиугольной призмы, имея значения длины ребра и высоты. Убедитесь, что ваши единицы измерения согласованы (например, если длина ребра измеряется в сантиметрах, то и высота должна быть измерена в сантиметрах).
Измеряя ребро призмы
Прежде всего, убедитесь, что у вас есть правильный инструмент для измерения ребра призмы. Используйте линейку или металлический штангенциркуль, чтобы быть уверенным в точности результатов.
Поместите ребро призмы на ровную поверхность и аккуратно разместите одну сторону инструмента на одном конце ребра. Затем медленно и аккуратно переместите другую сторону инструмента до противоположного конца ребра. Запишите полученное значение.
Важно учесть, что измерение должно быть произведено в единицах длины, которые будут использованы для вычисления объема призмы. Если измерение проводится в сантиметрах, то и объемы должны быть выражены в кубических сантиметрах.
Помните, что измерение ребра призмы должно быть достаточно точным, чтобы дать вам точный результат при вычислении объема. Запишите измерение и используйте его в последующих вычислениях.
Удачи в определении объема вашей шестиугольной призмы!
Подсчет объема шестиугольной призмы
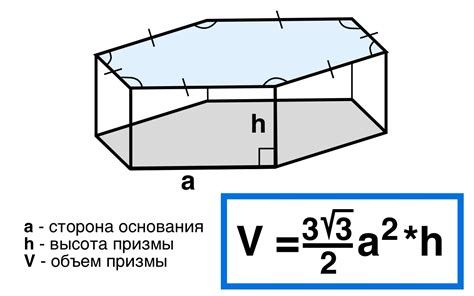
Объем шестиугольной призмы можно найти по формуле:
V = (3√3/2) * a * a * h
где V - объем призмы, a - длина ребра основания, h - высота призмы.
Чтобы подсчитать объем, необходимо узнать длину ребра основания и высоту призмы. После этого, подставив значения в формулу, можно найти объем шестиугольной призмы.
Таким образом, при знании длины ребра и высоты призмы можно легко подсчитать ее объем без лишних затрат времени и ресурсов.
Пример вычисления объема
Рассмотрим пример вычисления объема шестиугольной призмы через одно из ее ребер.
Для начала найдем площадь основания призмы. Чтобы это сделать, можно воспользоваться формулой площади правильного шестиугольника:
где - площадь основания, - длина ребра.
Затем найдем высоту призмы. Мы можем взять любое расстояние, перпендикулярное плоскостям основания и проведенное через центр шестиугольника. Например, если мы возьмем длину отрезка, соединяющего центр основания и одну из вершин, это будет одна из боковых высот . В случае правильной шестиугольной призмы, высота проходит через центр основания и перпендикулярна ему.
Итак, площадь основания равна , а высота равна .
Объем призмы можно найти, умножив площадь основания на высоту:
Таким образом, зная длину ребра призмы, мы можем легко вычислить ее объем без лишних затрат.
В данной статье мы рассмотрели способы нахождения объема шестиугольной призмы через ее ребро без лишних затрат.
Сначала мы ознакомились с основными свойствами шестиугольника и призмы, чтобы четко представлять себе структуру объекта, с которым будем работать.
Затем мы изучили метод нахождения площади основания призмы с помощью формулы для шестиугольника, а также вывели формулу для вычисления объема призмы через ребро и площадь основания.
Последним шагом было применение полученных формул на практике – рассмотрение примера и расчет объема шестиугольной призмы с известным значением ребра.
Теперь, благодаря этой статье, вы можете находить объем шестиугольной призмы через ее ребро и площадь основания без лишних затрат времени и усилий.