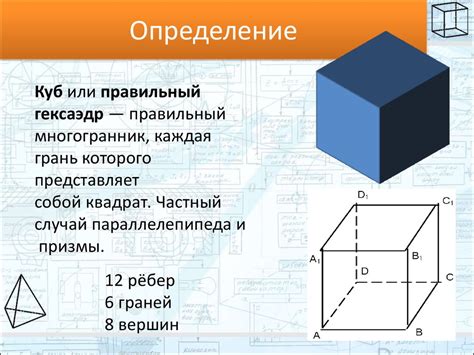
Куб - это геометрическое тело, которое имеет шесть граней, одинаковых по размеру и форме. У каждого ребра куба есть своя длина, и для того чтобы найти сумму всех ребер, нужно сложить длины всех шести ребер.
Для начала, необходимо знать длину одного ребра куба. Обычно она обозначается буквой "a". Если известна длина одного ребра, то можно легко найти длину остальных пяти ребер с помощью формулы. Так, длины всех ребер будут равны "a".
Следовательно, чтобы найти сумму всех ребер куба, нужно просто сложить шесть длин ребер, то есть умножить длину одного ребра на 6. Таким образом, формула для нахождения суммы всех ребер куба будет следующей: S = 6a, где "S" - это искомая сумма, а "a" - длина одного ребра куба.
Как найти сумму ребер куба

- Рассмотрим куб и обозначим его сторону a.
- В кубе есть 12 ребер.
- Каждое ребро имеет длину a.
Таким образом, чтобы найти сумму всех ребер куба, необходимо умножить длину каждого ребра на их количество:
Сумма ребер = длина ребра * количество ребер = a * 12.
Теперь вы знаете, как найти сумму всех ребер куба. Эта формула проста и легко применима для любого куба.
Определение и свойства куба
Основные свойства куба:
| 1. Формула для вычисления объема: | V = a^3 |
| 2. Формула для вычисления площади грани: | S = a^2 |
| 3. Формула для вычисления площади поверхности: | S_p = 6a^2 |
| 4. Диагональ куба: | d = a√3 |
Сумма всех ребер куба равна 12a, где a - длина ребра.
Также стоит отметить, что куб является особым случаем параллелепипеда, у которого все ребра равны. Он обладает симметрией относительно каждой из своих граней и имеет высокую степень симметрии.
Формула для расчета суммы ребер

Для нахождения суммы всех ребер куба существует простая и удобная математическая формула. Куб состоит из 12 ребер, каждое из которых имеет одинаковую длину. Таким образом, чтобы найти сумму всех ребер куба, нужно умножить длину одного ребра на 12.
Математически формула будет выглядеть следующим образом:
Сумма ребер куба = Длина ребра * 12
Где Сумма ребер куба - искомое значение, Длина ребра - длина одного из ребер куба. Выразив данную формулу, вы сможете быстро и легко получить ответ на вопрос о сумме всех ребер куба, даже если известны только его размеры.
Примеры вычисления суммы ребер

Для вычисления суммы всех ребер куба можно использовать формулу, учитывающую количество ребер. Куб имеет 12 ребер, поскольку каждая из 6 граней имеет по 2 ребра.
Пример вычисления суммы всех ребер куба:
Сумма ребер = Количество ребер × Длина одного ребра
Длина одного ребра в данном примере равна 1.
Сумма ребер = 12 * 1
Сумма ребер равна 12.
Таким образом, сумма всех ребер куба равна 12.
Практическое применение расчета суммы ребер
Расчет суммы всех ребер куба имеет практическое применение в различных областях, где требуется анализ геометрической структуры объектов. Ниже приведены несколько примеров, где этот расчет может быть полезен:
1. Архитектура и строительство:
При проектировании зданий и сооружений с использованием кубической формы, знание суммы ребер куба поможет получить представление о количестве материала, необходимого для его построения. Это позволит точнее оценить стоимость и избежать излишних затрат.
2. Инженерия и механика:
В промышленности и машиностроении сумма ребер куба может использоваться для определения жесткости или прочности конструкций. Расчет этой величины позволяет инженерам избежать возникновения несанкционированных движений, деформаций или поломок, которые могут привести к серьезным последствиям.
3. Компьютерная графика и моделирование:
В сфере компьютерной графики и моделирования сумма ребер куба может помочь определить сложность объектов и оценить вычислительную нагрузку при их отображении или создании анимации. Это позволяет программистам и дизайнерам оптимизировать процесс работы с графическими объектами и создать более реалистичные трехмерные модели.
4. Образование и научные исследования:
В образовательных учреждениях и научных институтах расчет суммы ребер куба может использоваться для обучения студентов и проведения экспериментов. Это помогает развить логическое мышление и понимание принципов геометрии и математики, а также способствует проведению различных исследований в разных областях науки.
Все вышеперечисленные применения демонстрируют важность расчета суммы ребер куба в различных сферах деятельности. Это позволяет получить более точную информацию о геометрическом объекте и помогает в принятии правильных решений при проектировании, строительстве, моделировании или обучении.