Окружность – это геометрическая фигура, состоящая из всех точек, равноудаленных от центра. Диаметр – это отрезок, соединяющий две точки на окружности и проходящий через ее центр. Хотите узнать, как вычислить окружность по ее диаметру? В этой статье мы раскроем перед вами все секреты этого простого и важного математического расчета.
Чтобы вычислить окружность по ее диаметру, нужно знать несколько простых формул. Одна из самых известных формул связывает диаметр окружности с ее радиусом. Радиус можно найти, разделив диаметр на два. Удивительно, но даже школьнику доступно вычислить окружность, зная диаметр, используя эту формулу.
Другая формула связывает радиус окружности и ее длину. Оказывается, длина окружности прямо пропорциональна радиусу и числу "пи" π. То есть, длину окружности можно найти, умножив радиус на два и на число π. Это может быть полезно, когда нужно вычислить длину серединного отрезка окружности по ее диаметру.
Как вычислить окружность по диаметру: шаг за шагом
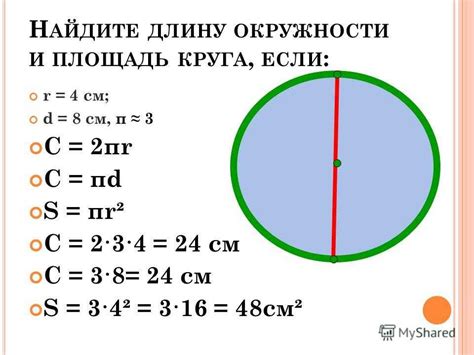
Шаг 1: Узнайте значение диаметра окружности. Диаметр – это прямая, соединяющая две противоположные точки на окружности. Обычно он обозначается буквой d.
Шаг 2: Используйте формулу для вычисления окружности по диаметру. Она выглядит следующим образом:
Окружность = π * d
В данной формуле π (Пи) – это математическая константа, примерное значение которой равно 3.14, а d – значение диаметра окружности.
Шаг 3: Подставьте значение диаметра в формулу и выполните вычисления. Например, если диаметр окружности равен 10 см, то:
Окружность = 3.14 * 10 = 31.4 см
Таким образом, окружность с диаметром 10 см имеет длину окружности, равную 31.4 см.
Обратите внимание, что результат показывает длину окружности, а не ее площадь. Для вычисления площади окружности необходимо использовать другую формулу.
Теперь, когда вы знаете, как вычислить окружность по диаметру, вы можете легко определить ее параметры в любой ситуации. Запомните, что формула контролирует точность ваших вычислений, поэтому следует использовать приближенное значение числа Пи.
Понятие окружности и диаметра
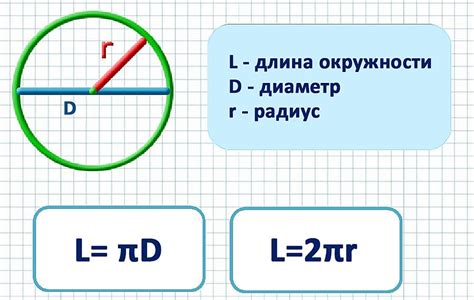
Диаметр - это отрезок, состоящий из двух точек окружности и проходящий через ее центр. Длина диаметра является наибольшей длиной, которую можно измерить на окружности.
Диаметр окружности является одним из основных параметров, по которому можно вычислить остальные характеристики окружности, такие как площадь и длина окружности. Он также является ключевым элементом при определении других геометрических фигур, образованных окружностями, таких как круги и секторы.
Зная диаметр окружности, можно легко вычислить ее радиус, который равен половине длины диаметра. Также, расстояние между центром окружности и любой точкой на ней будет равно радиусу.
Понимание понятия окружности и диаметра является важным для решения задач и заданий, связанных с геометрией и вычислениями параметров окружностей.
Формула нахождения окружности по диаметру
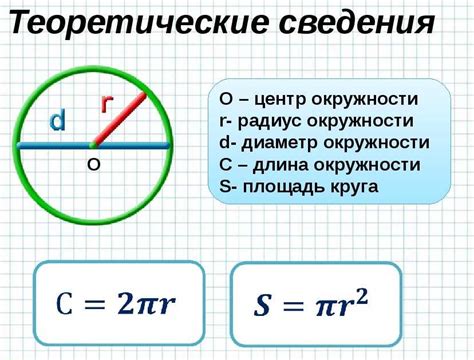
Длина окружности = π × диаметр
Здесь π (пи) - это математическая константа, примерное значение которой равно 3.14159. Оно соотносит длину окружности с ее диаметром.
Чтобы найти длину окружности, необходимо знать только ее диаметр. Подставьте значение диаметра в формулу, умножьте на π, и вы получите длину окружности.
Например, если диаметр окружности равен 10 сантиметрам, то длина окружности будет:
Длина окружности = 10 см × 3.14159 ≈ 31.4159 см
Таким образом, длина окружности равна примерно 31.4159 сантиметра.
Формула для нахождения окружности по диаметру основана на связи между этими двумя элементами геометрической фигуры. Она позволяет быстро и удобно вычислить длину окружности, используя только известное значение диаметра.
Примеры вычисления окружности по диаметру
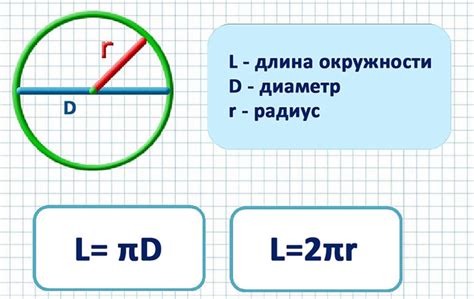
Длина окружности = π * диаметр
где π (пи) является математической константой, примерное значение которой равно 3,14159. Таким образом, чтобы вычислить длину окружности, нужно умножить диаметр на π.
Например, если диаметр окружности равен 10 сантиметрам, вы можете вычислить длину окружности следующим образом:
Длина окружности = 3,14159 * 10 см = 31,4159 см
Также можно вычислить площадь окружности, зная ее диаметр:
Площадь окружности = (π * (диаметр / 2)²)
где (диаметр / 2) - это радиус окружности.
Например, если диаметр окружности равен 10 сантиметрам, вы можете вычислить площадь окружности следующим образом:
Площадь окружности = (3,14159 * (10 / 2)²) = 3,14159 * 5² = 3,14159 * 25 = 78,53975
Теперь вы знаете две основные формулы для вычисления окружности по диаметру - длины окружности и площади окружности. Используйте их для решения геометрических задач и строительства различных конструкций.
Полезные советы и рекомендации

- При вычислении окружности по диаметру важно правильно определить значение диаметра. Убедитесь, что измерение произведено точно и нет ошибок при записи значения.
- Если возникают сомнения в точности измерения диаметра, рекомендуется повторить измерение несколько раз, используя разные инструменты для более точного результата.
- В случае если диаметр измерен с помощью неидеального инструмента, рекомендуется произвести среднее арифметическое нескольких измерений для достижения более точного значения.
- При проведении вычислений используйте формулу для вычисления окружности по диаметру: окружность = π * d, где d - диаметр окружности.
- Не забывайте, что число π - это приблизительно 3,14159. Для более точных вычислений можно использовать более точное значение этого числа.
- При округлении полученного значения окружности, учитывайте требования задачи или контекста, в котором производятся вычисления.
- Если необходимо вывести результат вычислений, убедитесь, что единицы измерения окружности (например, см, м, км) указаны явно, чтобы избежать путаницы.
- Постарайтесь проверить правильность вычислений, используя другие методы или инструменты, чтобы удостовериться в их точности.
- Не забывайте, что решение задачи вычисления окружности по диаметру полезно не только в математическом контексте, но и может использоваться в различных практических ситуациях, например, в строительстве или дизайне.