Равнобедренный треугольник - это треугольник, у которого две стороны имеют одинаковую длину. Один из ключевых параметров этого треугольника - это его основание, то есть сторона, относительно которой измеряются другие две стороны.
Найти основание равнобедренного треугольника по сторонам можно несколькими способами. Один из них - применение теоремы Пифагора, которая устанавливает соотношение между длинами сторон треугольника. Она гласит, что квадрат длины гипотенузы (самой длинной стороны) равен сумме квадратов длин двух других сторон.
Для нахождения основания равнобедренного треугольника сначала нужно найти длины его сторон. Затем, используя формулу Пифагора, вычислить длину гипотенузы. Далее, зная длину гипотенузы и одинаковые длины боковых сторон, можно определить длину основания, вычитая удвоенную длину боковой стороны из длины гипотенузы.
Методы определения основания равнобедренного треугольника по сторонам
Метод 1: Использование формулы для длины основания
Для равнобедренного треугольника с длиной основания a и длиной боковой стороны b, длина основания может быть определена с использованием следующей формулы:
a = 2 * sqrt(b^2 - (b/2)^2)
Например, если длина боковой стороны равна 8, то длина основания будет:
a = 2 * sqrt(8^2 - (8/2)^2) = 2 * sqrt(64 - 16) = 2 * sqrt(48) ≈ 13.86
Метод 2: Использование теоремы Пифагора
Для равнобедренного треугольника с длиной боковой стороны b и длиной основания a, с использованием теоремы Пифагора можно определить длину основания:
a = sqrt(4 * b^2 - b^2) = sqrt(3 * b^2)
Например, если длина боковой стороны равна 5, то длина основания будет:
a = sqrt(4 * 5^2 - 5^2) = sqrt(4 * 25 - 25) = sqrt(75) ≈ 8.66
Метод 3: Использование свойств равнобедренного треугольника
Другим методом определения основания равнобедренного треугольника по сторонам является использование следующих свойств:
- Боковые стороны равны между собой;
- Углы при основании равны;
- Сумма углов треугольника равна 180 градусов.
Исходя из этих свойств, можно определить длину основания путем решения системы уравнений или с использованием геометрических конструкций.
Высота и биссектриса как основные пути определения основания

Высота - это отрезок, проведенный из вершины треугольника до основания, перпендикулярно самому основанию. Для нахождения высоты равнобедренного треугольника можно использовать теорему Пифагора или применить геометрический подход. В первом случае, длина высоты будет равна квадратному корню из разности квадратов половины основания и половины стороны треугольника. Во втором случае, достаточно провести перпендикуляр из вершины треугольника к середине основания.
Биссектриса - это отрезок, проведенный из вершины треугольника к противоположной стороне и разделяющий эту сторону на два равных отрезка. Для нахождения биссектрисы равнобедренного треугольника можно воспользоваться теоремой углового биссектрисы или применить геометрический подход. В первом случае, длина биссектрисы будет равна произведению длины основания на косинус половины угла при вершине треугольника. Во втором случае, достаточно провести биссектрису угла при основании равнобедренного треугольника и измерить ее длину.
Какой метод использовать для определения основания равнобедренного треугольника зависит от доступных данных и предпочтений геометра. Выбор метода может быть обусловлен как удобством его применения, так и наличием дополнительных условий, например, известной длины биссектрисы или высоты.
Связь между основанием равнобедренного треугольника и его углами
В равнобедренном треугольнике углы при основании равны. Это означает, что если мы знаем величину одного из углов, мы можем найти значение двух других углов. Для этого мы можем использовать формулу:
| Угол при основании | Другие два угла |
|---|---|
| 60° | 60° |
| 70° | 55° |
| 80° | 50° |
Для измерения углов в треугольнике можно использовать геометрические инструменты, такие как транспортир. Если известны два угла треугольника, можно вычислить третий, вычитая сумму первых двух углов из 180°.
Зная значения углов, мы можем найти длину основания равнобедренного треугольника с помощью геометрических формул и теорем. Например, если мы знаем длину боковой стороны и угол при основании, можем использовать тригонометрию для расчета длины основания:
Основание = 2 * сторона * sin(угол при основании/2)
Таким образом, связь между основанием равнобедренного треугольника и его углами играет важную роль в решении задач, связанных с этим видом треугольников. Зная углы, мы можем найти длину основания и решить различные геометрические задачи.
Определение основания через теорему косинусов
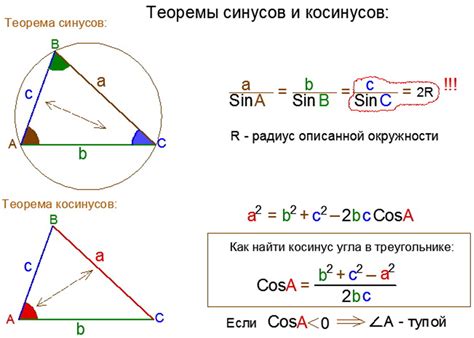
Для равнобедренного треугольника, в котором две стороны равны, мы можем использовать теорему косинусов, чтобы найти длину основания. Для этого нам понадобятся следующие параметры:
- Значение угла между основанием и одной из равных сторон треугольника
- Длина одной из равных сторон треугольника
Пользуясь теоремой косинусов, мы можем выразить длину основания через известные параметры. Формула выглядит следующим образом:
b = 2 * a * cos(α/2)
Где:
- b - длина основания
- a - длина равных сторон треугольника
- α - угол между основанием и одной из равных сторон, выраженный в радианах
Применение теоремы косинусов позволяет быстро и точно определить длину основания равнобедренного треугольника, если известны длина равных сторон и значение угла между ними.
Способ нахождения основания с использованием теоремы Пифагора
Один из способов определить основание равнобедренного треугольника заключается в использовании теоремы Пифагора.
Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
В случае равнобедренного треугольника, две стороны являются равными и являются катетами прямоугольного треугольника, образованного половиной основания и высотой треугольника. Гипотенуза этого прямоугольного треугольника соответствует длине основания равнобедренного треугольника.
Используя данную информацию, мы можем найти основание равнобедренного треугольника, зная длину одной из сторон и высоту.
Для этого нужно:
1. Возвести в квадрат длину стороны и разделить полученное значение на 4.
2. Вычесть из этого значения квадрат высоты и извлечь корень.
Таким образом, получим длину основания равнобедренного треугольника.
Приведем пример. Пусть у нас есть равнобедренный треугольник, у которого сторона равна 6 и высота равна 4.
1. Возводим 6 в квадрат и получаем 36.
2. Делим 36 на 4 и получаем 9.
3. Вычитаем из 9 квадрат 4 и получаем 5.
4. Извлекаем корень из 5 и получаем 2,24.
Таким образом, основание равнобедренного треугольника равно 2,24.
Таким образом, вычисление основания равнобедренного треугольника с использованием теоремы Пифагора является простым и эффективным методом.
Примеры расчета основания равнобедренного треугольника
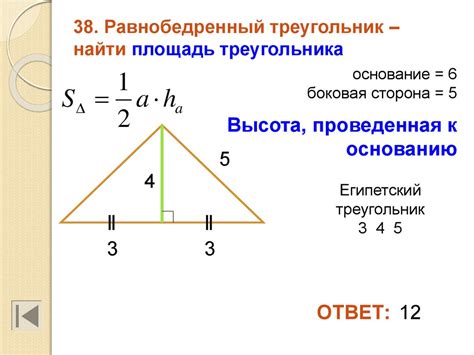
Рассмотрим несколько примеров расчета основания равнобедренного треугольника. Для наглядности, возьмем известные значения длин сторон и найдем основание треугольника.
- Пример 1:
- Пример 2:
- Пример 3:
Дано: сторона AB = 8 см, сторона AC = 6 см.
Решение: для равнобедренного треугольника, сторона AB и сторона AC должны быть равны. В данном случае, сторона AB = 8 см, а сторона AC = 6 см. Таким образом, сторона AB является основанием треугольника.
Дано: сторона AB = 5 см, сторона AC = 5 см.
Решение: опять же, для равнобедренного треугольника, сторона AB и сторона AC должны быть равны. В данном случае, обе стороны равны 5 см. Основание треугольника совпадает с любой из этих сторон.
Дано: сторона AB = 10 см, сторона AC = 7 см.
Решение: так как сторона AB и сторона AC не равны, этот треугольник не является равнобедренным. В этом случае нет основания треугольника, так как основание определяется как одна из равных сторон.
Из примеров видно, что основание равнобедренного треугольника является одной из равных сторон треугольника. Если все стороны равны, то любая из них может быть основанием. Если стороны не равны, то треугольник не является равнобедренным и не имеет основания.
Практическое применение знания основания равнобедренного треугольника
Одним из таких примеров практического применения знания основания равнобедренного треугольника является строительство крыши на доме. Знание основания равнобедренного треугольника позволяет определить длину боковой стороны и установить нужный угол наклона крыши. Таким образом, строитель может точно рассчитать материалы и выполнить работу без излишних затрат времени и денег.
Другим примером применения знания основания равнобедренного треугольника является дизайн интерьера. Знание основания позволяет архитекторам и дизайнерам выбирать оптимальные формы и соотношения для создания гармоничного и эстетически привлекательного пространства. Например, основание равнобедренного треугольника может быть использовано для создания интересных и симметричных композиций в мебели, декоре или освещении.
Также, знание основания равнобедренного треугольника может быть применено в архитектуре для создания устойчивых и прочных конструкций. Зная длину основания, архитектор может рассчитать подходящую ширину или длину опоры, чтобы обеспечить устойчивость и надежность сооружения.
В образовательной сфере знание основания равнобедренного треугольника используется при изучении геометрии и решении геометрических задач. Это свойство треугольника помогает студентам лучше понять теорию и развить логическое мышление.
| Примеры применения основания равнобедренного треугольника: |
|---|
| Строительство крыши |
| Дизайн интерьера |
| Архитектурные конструкции |
| Образовательные задачи по геометрии |