Треугольник - это геометрическая фигура, состоящая из трех сторон и трех углов. Знание отношения сторон треугольника к его углам является важным элементом в геометрии. Правильный расчет отношения сторон помогает определить форму и свойства треугольника.
Определить отношение сторон треугольника можно с помощью соотношения, называемого теоремой синусов. Согласно этой теореме, отношение длины каждой стороны треугольника к синусу противолежащего ей угла является постоянным.
Таким образом, для нахождения отношения сторон треугольника, необходимо измерить все три угла. Затем, используя теорему синусов, можно составить уравнение и вычислить длины сторон треугольника.
Использование этой теоремы является эффективным способом для нахождения отношения сторон треугольника по углам. Оно может быть применено в различных задачах геометрии, включая нахождение периметра, площади или других свойств треугольников.
Как вычислить отношение сторон треугольника?

Отношение сторон треугольника можно вычислить, зная значения его углов. Для этого необходимо использовать тригонометрические функции, такие как синус, косинус и тангенс.
Сначала найдите значение каждого угла треугольника. Затем примените следующие формулы:
1. Для нахождения отношения между сторонами, противолежащими двум углам, используйте правило синусов:
a/sin(A) = b/sin(B) = c/sin(C)
2. Для нахождения отношения между сторонами и синусами углов выберите одну сторону в качестве "основы" и умножьте ее на синус противолежащего угла:
a/sin(A) = b/sin(B) = c/sin(C)
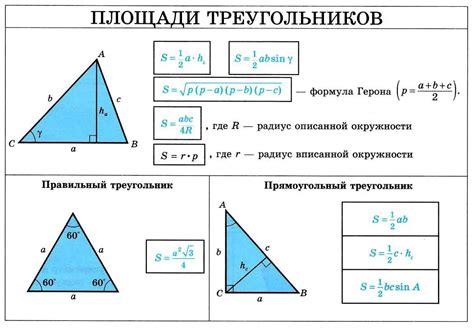
3. Для нахождения отношения между окружностью, вписанной в треугольник, и радиусами вписанных окружностей используйте формулу:
R/r = (a + b + c) / 2S
Где "a", "b" и "c" - это стороны треугольника, "A", "B" и "C" - углы треугольника, "R" - радиус окружности, вписанной в треугольник, "r" - радиус одной из вписанных окружностей, "S" - площадь треугольника.
Эти формулы позволяют найти отношение сторон треугольника и способствуют пониманию его геометрических свойств.
Подробное объяснение

Существует несколько способов вычисления отношения сторон треугольника по углам:
- Теорема синусов: основное отношение, которое связывает стороны и углы треугольника. Формула звучит следующим образом: синус угла α деленный на сторону a равен синусу угла β деленному на сторону b, и так далее.
- Теорема косинусов: это более общий случай теоремы синусов. Она связывает стороны и углы треугольника с помощью косинусов. Формула звучит следующим образом: квадрат стороны a равен сумме квадратов сторон b и c минус произведение сторон b и c на косинус угла α, и так далее.
- Тангенс угла: это отношение стороны, противолежащей углу, к стороне, прилежащей углу. Формула звучит следующим образом: тангенс угла α равен противолежащей стороне a деленной на прилежащую сторону b, и так далее.
Вычисление отношения сторон треугольника по углам является важным инструментом для решения различных задач, связанных с геометрией и треугольниками. Зная отношение сторон, можно рассчитать длину сторон треугольника, площадь треугольника и другие характеристики.
Формула вычисления отношения сторон треугольника
Отношение сторон треугольника можно вычислить с использованием тригонометрических функций и известных углов треугольника. Для этого существует специальная формула, называемая теоремой синусов. Она позволяет выразить отношение длин сторон треугольника через синусы соответствующих углов.
Если в треугольнике заданы два угла и сторона, находящаяся между ними, то отношение этой стороны к синусам данных углов равно отношению двух других сторон треугольника к синусу третьего угла.
Теорема синусов имеет следующий вид:
a/sin(A) = b/sin(B) = c/sin(C)
Где:
- a, b, c - длины сторон треугольника;
- A, B, C - величины соответствующих углов;
Используя данную формулу, можно рассчитать отношение сторон треугольника по известным углам. Для этого необходимо знать длины двух сторон треугольника и величины двух углов, соединенных этими сторонами. Подставив значения в формулу, можно вычислить отношение сторон треугольника.
Формула синусов является важным инструментом для решения задач треугольников и нахождения неизвестных длин сторон.