Пирамиды – это уникальные геометрические фигуры, которые привлекают внимание своей необычной формой и симметрией. Они состоят из трехмерных элементов, включая ребра, вершины и грани. Одной из наиболее интересных задач, связанных с пирамидами, является поиск точки пересечения прямой и плоскости внутри пирамиды.
Найдя точку пересечения, можно решить множество задач, связанных с различными областями, такими как геометрия, архитектура и дизайн. Она поможет определить расположение объектов внутри пирамиды и решить разнообразные геометрические задачи.
Но как найти точку пересечения прямой и плоскости в пирамиде? Существует несколько подходов к решению этой задачи, которые могут быть полезными для понимания и работы с пирамидами. В этой статье мы рассмотрим некоторые полезные советы и инструкции, которые помогут вам справиться с этой задачей.
Определение точки пересечения
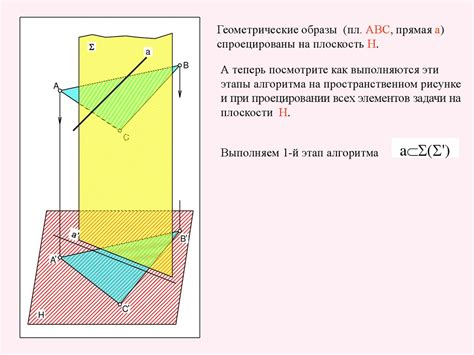
Шаг 2: Запишите уравнение прямой в параметрическом виде, задав две точки на прямой. Например, прямая может быть задана в виде:
x = x0 + at
y = y0 + bt
z = z0 + ct
где (x0, y0, z0) - точка на прямой, (a, b, c) - направляющий вектор прямой.
Шаг 3: Подставьте уравнение прямой в уравнение плоскости, чтобы получить уравнение вида:
(A(x0 + at) + B(y0 + bt) + C(z0 + ct) + D) = 0
Раскройте скобки и приведите подобные слагаемые.
Шаг 4: Решите полученное уравнение относительно параметра t. Если уравнение имеет решение, то найдена точка пересечения прямой и плоскости.
Шаг 5: Подставьте найденное значение параметра t в уравнение прямой, чтобы найти координаты точки пересечения. Уравнение прямой в параметрическом виде позволяет найти координаты точки при заданном значении параметра t.
Важность правильного определения точки пересечения
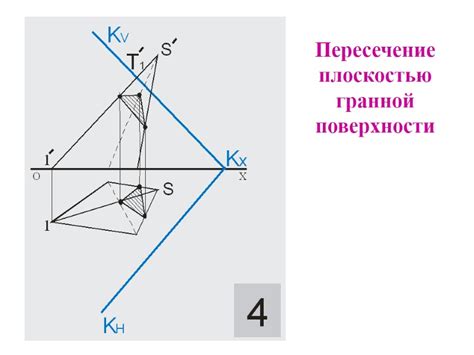
Корректное определение точки пересечения играет важную роль в процессе проектирования и моделирования объектов. Например, представьте себе задачу создания трехмерной модели здания. Точное определение точки пересечения прямой, которая представляет стены, и плоскости, которые представляют полы и потолки, позволит реалистично отразить структуру здания и взаимное расположение его элементов.
Точка пересечения также может быть использована для определения длины отрезка, который соединяет объекты или точки в пространстве. Это может быть полезно при решении различных геометрических задач, таких как определение расстояния между двумя объектами или определение геометрических параметров объектов.
Правильное определение точки пересечения также имеет практическое применение в инженерии и строительстве. Например, при проектировании дорожных сетей или сетей водопровода, точное определение точки пересечения помогает определить оптимальное расположение трассы дороги или трубопровода, обеспечивая минимальные затраты и максимальную эффективность.
В общем, точное определение точки пересечения прямой и плоскости в пирамиде является важным инструментом для решения различных задач геометрии, инженерии и моделирования. Правильное определение этой точки позволяет получить точные результаты и упрощает процесс решения задач.
Советы для нахождения точки пересечения

Прежде чем приступить к нахождению точки пересечения прямой и плоскости в пирамиде, обратите внимание на следующие советы:
1. Определите уравнение прямой:
Для того чтобы найти точку пересечения, необходимо знать уравнение прямой. Это может быть уравнение в параметрической форме или в канонической форме. В зависимости от того, как дано уравнение прямой, вам потребуется выполнить соответствующие шаги.
2. Найдите уравнение плоскости:
На втором шаге вам необходимо определить уравнение плоскости, с которой планируется найти пересечение. Уравнение плоскости может быть дано в нормальной форме, параметрической форме или в канонической форме. В зависимости от формы уравнения вам потребуется выбрать соответствующий метод.
3. Решите систему уравнений:
После определения уравнения прямой и плоскости вы можете составить систему уравнений. Подставив уравнение прямой в уравнение плоскости, вы сможете получить систему уравнений, которую можно решить для нахождения точки пересечения.
4. Примените метод решения системы уравнений:
Существуют различные методы решения системы уравнений, такие как метод подстановки, метод исключения или графический метод. Выберите наиболее удобный для вас метод и примените его для решения системы уравнений и нахождения точки пересечения.
5. Проверьте полученный результат:
В конечном итоге, когда вы найдете точку пересечения, не забудьте проверить свой результат. Подставьте найденные координаты точки в уравнение прямой и плоскости, чтобы убедиться, что они удовлетворяют обоим уравнениям.
Следуя этим советам, вы сможете более эффективно находить точку пересечения прямой и плоскости в пирамиде.
Инструкция по нахождению точки пересечения
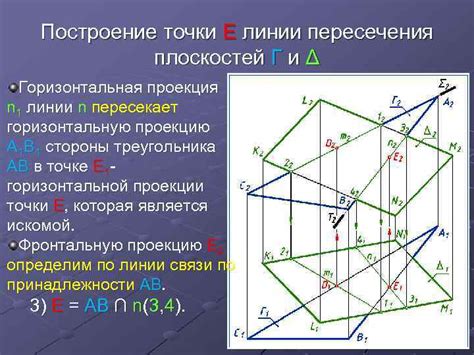
Для того чтобы найти точку пересечения прямой и плоскости в пирамиде, следуйте этим шагам:
- Задайте уравнение плоскости, с которой пересекается прямая. Уравнение плоскости обычно имеет вид Ax + By + Cz + D = 0, где A, B и C - коэффициенты плоскости, а D - свободный член.
- Задайте параметрическое уравнение прямой. Обычно параметрическое уравнение прямой можно записать как x = x₀ + at, y = y₀ + bt, z = z₀ + ct, где (x₀, y₀, z₀) - координаты начальной точки прямой, а (a, b, c) - направляющий вектор прямой.
- Подставьте параметрическое уравнение прямой в уравнение плоскости и решите полученное уравнение относительно параметра t. Это даст координаты точки пересечения прямой и плоскости.
- Проверьте, лежит ли найденная точка пересечения внутри пирамиды или на ее поверхности. Если точка находится внутри пирамиды, она является точкой пересечения прямой и плоскости. Если точка находится на поверхности пирамиды, рассмотрите другую часть пирамиды, чтобы найти точку пересечения внутри нее.
Следуя этой инструкции, вы сможете найти точку пересечения прямой и плоскости в пирамиде.
Примеры решения задачи нахождения точки пересечения

В этом разделе приведены несколько примеров решения задачи нахождения точки пересечения прямой и плоскости в пирамиде. Каждый пример сопровождается подробным описанием шагов и математическими выкладками.
| Пример | Описание решения |
|---|---|
| Пример 1 | В данном примере необходимо найти точку пересечения прямой, заданной уравнениями x = 2t, y = 3t, z = 4t, и плоскости, заданной уравнением x + 2y + 3z = 10. Для начала подставим параметрические уравнения прямой в уравнение плоскости и решим полученную систему уравнений относительно t. Затем найдем значения x, y и z с помощью найденного значения t и подставим их в исходные уравнения прямой. |
| Пример 2 | В этом примере необходимо найти точку пересечения прямой, заданной уравнениями x = 3t, y = 2t, z = t, и плоскости, заданной уравнением 2x + y - z = 5. Аналогично первому примеру, мы подставим параметрические уравнения прямой в уравнение плоскости и решим полученную систему уравнений относительно t. Затем найдем значения x, y и z с помощью найденного значения t и подставим их в исходные уравнения прямой. |
| Пример 3 | В данном примере необходимо найти точку пересечения прямой, заданной уравнениями x = t, y = t, z = t, и плоскости, заданной уравнением x + y + z = 2. Подставим параметрические уравнения прямой в уравнение плоскости и решим полученную систему уравнений относительно t. Затем найдем значения x, y и z с помощью найденного значения t и подставим их в исходные уравнения прямой. |
Данные примеры позволяют наглядно продемонстрировать процесс нахождения точки пересечения прямой и плоскости в пирамиде и помогут разобраться в данной теме.