Периметр и площадь – это два важных показателя, которые позволяют определить размеры геометрических фигур. Они могут быть различными для разных фигур с разными сторонами. Знание формул и правил расчета позволит нам точно определить эти значения.
Существуют различные формулы для нахождения периметра и площади различных фигур. Например, для прямоугольника периметр вычисляется как сумма длин всех его сторон, а площадь равна произведению длин его сторон. Для треугольника периметр находится как сумма длин всех его сторон, а площадь – через полупериметр и радиусы вписанной и описанной окружностей.
Для расчета периметра и площади фигуры с разными сторонами необходимо разобраться в основных правилах и использовать соответствующие формулы. Таким образом, мы сможем точно определить эти показатели и применить их при решении практических задач.
Основные понятия
Периметр фигуры – это сумма длин всех ее сторон. Он позволяет нам определить длину контура или границы фигуры.
Площадь фигуры – это понятие, используемое для измерения поверхности фигуры. Она определяет, как много пространства занимает фигура.
Для фигур с разными сторонами, периметр и площадь будут рассчитываться по-разному. Например, для прямоугольника периметр вычисляется путем сложения длин всех его сторон, а площадь – путем умножения его длины на ширину. Для треугольника периметр вычисляется путем сложения длин всех его сторон, а площадь – путем умножения половины основания на высоту.
Как найти периметр фигуры
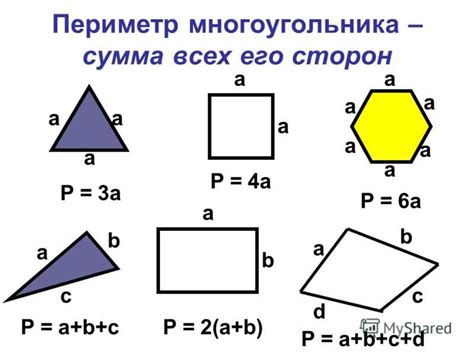
Для прямоугольника периметр рассчитывается по формуле:
Периметр = 2 * (длина + ширина).
Для квадрата, имеющего одинаковые стороны, периметр можно рассчитать так:
Периметр = 4 * сторона.
Если в фигуре присутствуют более одной стороны, то периметр можно найти, сложив длины всех сторон.
Одним из способов найти периметр фигуры со сложной формой является представление его в виде набора прямоугольников и треугольников. В этом случае периметр найдется суммированием длин всех прямоугольников и треугольников.
Например, если фигура содержит стороны a, b, c, d, то ее периметр будет равен:
Периметр = a + b + c + d.
Важно помнить, что вершины фигуры не должны быть загнутыми или выгнутыми, иначе формула расчета периметра будет другой.
Как найти площадь фигуры
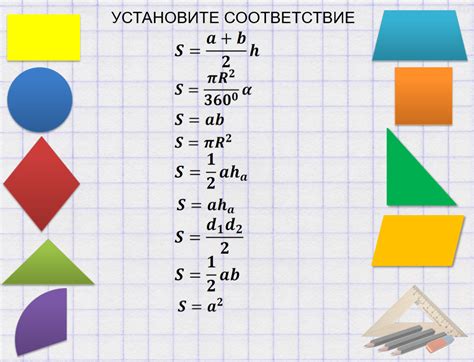
Для нахождения площади фигуры необходимо знать ее форму и соответствующую формулу. В зависимости от типа фигуры существуют различные способы вычисления площади.
Например, для прямоугольника площадь вычисляется как произведение длины на ширину. Формула для прямоугольника: S = a * b, где a - длина, b - ширина.
Для треугольника площадь можно найти используя формулу Герона, которая основывается на известных сторонах треугольника и полупериметре. Формула Герона: S = √(p * (p - a) * (p - b) * (p - c)), где a, b и c - стороны треугольника, p - полупериметр.
Для круга площадь вычисляется по формуле S = π * r^2, где π - число π (примерно 3,14), r - радиус круга.
Вычисление площади фигуры требует знания ее характеристик и подходящей формулы. Поэтому перед вычислением рекомендуется определить тип фигуры и выбрать соответствующую формулу.
Как найти периметр и площадь треугольника
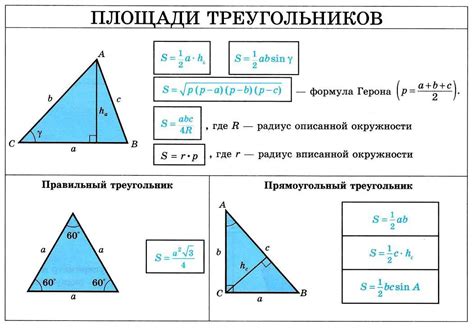
Периметр треугольника - это сумма длин всех его сторон. Чтобы найти периметр треугольника, нужно просто сложить длины всех его сторон.
Площадь треугольника - это площадь пространства, ограниченного его сторонами. Существует несколько различных методов для вычисления площади треугольника в зависимости от известных данных:
- Метод полупериметра: площадь треугольника можно вычислить, зная его полупериметр (периметр, разделенный на 2) и длины его сторон. Формула для вычисления площади треугольника по полупериметру выглядит следующим образом: S = sqrt(p * (p - a) * (p - b) * (p - c)), где S - площадь треугольника, p - полупериметр, a, b, c - длины сторон треугольника.
- Метод высоты: если известна высота треугольника (отрезок, опущенный из вершины к противолежащей стороне), площадь треугольника можно найти, умножив длину этой высоты на половину длины противолежащей стороны. Формула для вычисления площади треугольника по высоте выглядит следующим образом: S = (h * b) / 2, где S - площадь треугольника, h - высота треугольника, b - длина противолежащей стороны.
Найдя периметр и площадь треугольника, можно использовать эти значения для решения различных задач и проблем. К примеру, для строительства или написания программного кода.
Изучение математики и геометрии помогает нам лучше понять мир вокруг нас и использовать его знания в повседневной жизни.
Как найти периметр и площадь прямоугольника
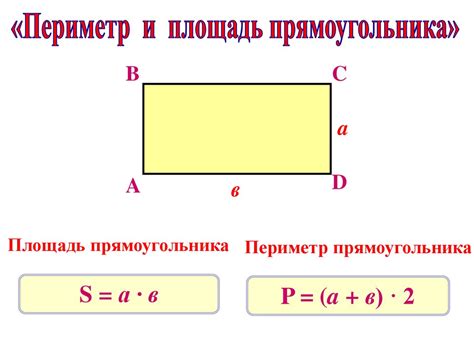
Для того чтобы найти периметр прямоугольника, необходимо сложить длины все его сторон. Если стороны прямоугольника обозначены символами a и b, то периметр можно выразить следующей формулой: P = 2a + 2b.
Чтобы найти площадь прямоугольника, необходимо умножить длину одной из его сторон на длину другой стороны. Если стороны прямоугольника обозначены символами a и b, то площадь можно вычислить следующей формулой: S = a * b.
Например, у нас есть прямоугольник со сторонами a = 4 см и b = 6 см. Тогда его периметр будет равен P = 2 * 4 + 2 * 6 = 8 + 12 = 20 см, а площадь - S = 4 * 6 = 24 см².
Теперь вы знаете, как найти периметр и площадь прямоугольника. Эта информация может быть полезной во многих задачах, связанных с геометрией и строительством.
Как найти периметр и площадь круга
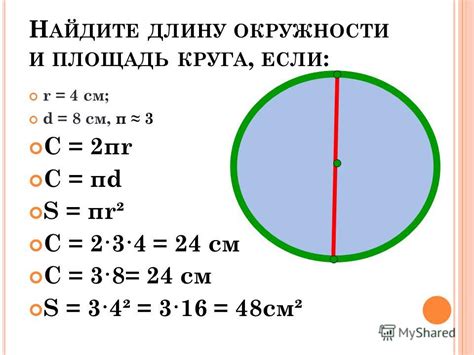
Периметр круга - это длина его окружности, то есть расстояние вокруг него. Формула для нахождения периметра круга упрощается следующим образом:
периметр = 2 * π * радиус
где π (пи) - математическая константа, приближенно равная 3.14 или 22/7.
Для нахождения площади круга используется следующая формула:
площадь = π * радиус²
Чтобы найти площадь круга, нужно умножить значение π (пи) на квадрат радиуса.
Например, если радиус круга равен 5, то для нахождения его периметра мы будем использовать формулу:
периметр = 2 * 3.14 * 5 = 31.4
А для нахождения площади круга применим формулу:
площадь = 3.14 * 5² = 78.5
Теперь вы знаете, как найти периметр и площадь круга, используя соответствующие формулы. Эти концепции могут быть полезными при решении задач, связанных с геометрией и измерением поверхности круговых объектов.