Ромб – это геометрическая фигура, состоящая из четырех равных сторон. Периметр ромба – это сумма длин всех его сторон. Однако, эта задача может быть сложнее, если известны только диагонали ромба. В этой статье мы подробно объясним, как вычислить периметр ромба, когда известны его диагонали.
Для вычисления периметра ромба по диагоналям, нам понадобится использовать некоторые теоретические знания о свойствах ромбов. Во-первых, диагонали ромба взаимно перпендикулярны и делят его на четыре равных треугольника. Следовательно, длины диагоналей ромба являются основаниями этих треугольников.
Для вычисления периметра ромба, мы можем воспользоваться формулой, которая учитывает длины сторон треугольников, образованных диагоналями ромба. Периметр ромба вычисляется путем удвоения суммы длин сторон одного из треугольников. Таким образом, мы можем найти одну сторону ромба, умножить ее на 4 и получить итоговый периметр ромба.
Определение ромба и его особенности
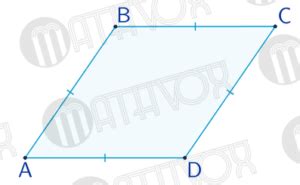
Основными особенностями ромба являются:
- Равенство диагоналей: в ромбе диагонали делятся пополам и взаимно перпендикулярны. Это значит, что каждая диагональ делит ромб на два равных треугольника, а также является осью симметрии ромба.
- Равные стороны: все стороны ромба имеют одинаковую длину, поэтому его периметр можно вычислить, умножив длину одной стороны на 4.
- Равные углы: все углы ромба равны между собой и составляют 90 градусов. Это делает ромб похожим на квадрат, но с наклонными сторонами и более широким диагоналями.
Зная эти особенности ромба, мы можем приступить к вычислению его периметра по диагоналям. Это позволяет нам определить длину каждой стороны и, далее, вычислить периметр, который представляет собой сумму длин всех сторон ромба.
Свойства диагоналей ромба

Диагонали ромба делят его на четыре равных треугольника. Особенностью ромба является то, что диагонали ромбово перпендикулярны друг другу. Это значит, что угол между диагоналями ромба равен 90 градусов.
Также стоит отметить, что диагональ ромба является его осью симметрии. Это означает, что при отражении ромба относительно его диагонали, фигура совпадает с исходным ромбом.
Еще одно свойство диагоналей ромба - они делят его на четыре равных треугольника. Это означает, что площади этих треугольников будут равны и могут быть вычислены по формуле: площадь треугольника = (диагональ1 * диагональ2) / 2.
| Свойство | Значение |
|---|---|
| Диагонали равны между собой | Д1 = Д2 |
| Угол между диагоналями | 90° |
| Диагональ - ось симметрии ромба | Диагональ делит фигуру на две симметричные половины |
| Площадь ромба | П=(Д1*Д2)/2 |
Зная эти свойства, можно эффективно использовать их для вычисления периметра ромба или других параметров данной фигуры.
Разбор формулы нахождения периметра ромба
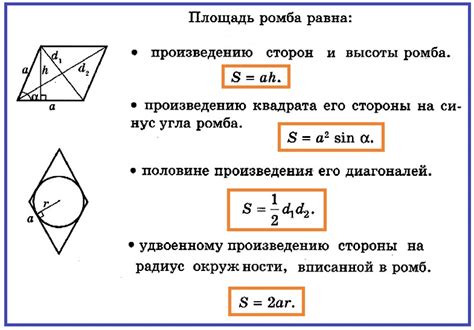
Если известны длины диагоналей ромба, то периметр можно вычислить по следующей формуле:
- Найдите половину произведения длин диагоналей: (d1 * d2) / 2
- Умножьте полученное значение на 2
Если известна длина одной стороны ромба, то периметр можно вычислить так:
- Примените формулу: 4 * a, где a – длина одной стороны ромба.
Если известны площадь и длина одной стороны ромба, то периметр можно вычислить следующим образом:
- Найдите длину одной стороны: a = √(S / h), где S – площадь ромба, а h – расстояние от одной из вершин до противоположной диагонали.
- Умножьте полученное значение на 4
Зная эти формулы, вы сможете легко находить периметр ромба в зависимости от имеющихся данных. Однако, помните, что для правильного применения формулы необходимо знание всех соответствующих параметров ромба.
Шаги по нахождению периметра ромба по диагоналям
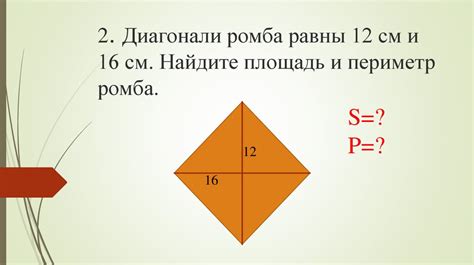
Для нахождения периметра ромба по заданным диагоналям, необходимо выполнить следующие шаги:
- Найдите длины диагоналей ромба. Для этого можно использовать уже известную формулу для длины диагонали ромба: d = sqrt((a^2 + b^2)/2), где d - длина диагонали, a и b - стороны ромба.
- Вычислите полупериметр ромба, сложив длины всех его сторон: S = a + b + c + d, где S - полупериметр, a, b, c и d - стороны ромба.
- Умножьте полупериметр ромба на 2, чтобы получить периметр: P = 2S, где P - периметр.
После выполнения этих шагов, вы получите периметр ромба по заданным диагоналям.
Пример расчета периметра ромба
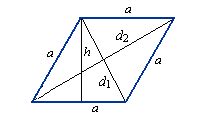
Для расчета периметра ромба необходимо знать значение длин двух его диагоналей. Пусть длина первой диагонали равна d₁, а длина второй диагонали равна d₂.
Периметр ромба вычисляется по формуле:
P = 4a, где a - длина стороны ромба.
Для определения длины стороны ромба можно использовать следующую формулу:
a = √(d₁² + d₂²) / 2.
Сначала вычислим длину стороны ромба по данным диагоналям:
a = √(d₁² + d₂²) / 2.
Затем найдем периметр ромба:
P = 4a.
Таким образом, мы можем найти периметр ромба по известным значениям его диагоналей.
Закрепление материала на практике
Теперь, чтобы закрепить полученные знания, давайте рассмотрим несколько практических примеров расчета периметра ромба по диагоналям.
Пример 1:
Допустим, у нас есть ромб со стороной a = 6 см и диагоналями d1 = 8 см и d2 = 10 см. Найдем периметр.
Сначала найдем половину длины первой диагонали (d1/2) и половину длины второй диагонали (d2/2):
d1/2 = 8/2 = 4 см
d2/2 = 10/2 = 5 см
Теперь используем формулу для расчета периметра ромба по диагоналям:
периметр = 2√(d1/2)^2 + (d2/2)^2)
периметр = 2√(4^2 + 5^2)
периметр = 2√(16 + 25)
периметр = 2√41
Округляем полученный результат до нужной точности и получаем окончательный ответ:
периметр ≈ 15.27 см
Пример 2:
Рассмотрим ромб со стороной a = 12 см и диагоналями d1 = 16 см и d2 = 20 см. Найдем периметр.
Сначала найдем половину длины первой диагонали (d1/2) и половину длины второй диагонали (d2/2):
d1/2 = 16/2 = 8 см
d2/2 = 20/2 = 10 см
Теперь используем формулу для расчета периметра ромба по диагоналям:
периметр = 2√(d1/2)^2 + (d2/2)^2)
периметр = 2√(8^2 + 10^2)
периметр = 2√(64 + 100)
периметр = 2√164
Округляем полученный результат до нужной точности и получаем окончательный ответ:
периметр ≈ 39.25 см
Таким образом, мы можем применять формулу для нахождения периметра ромба по диагоналям на практике, используя данные о длинах стороны и диагоналей ромба. Калькулятор или компьютер с программой для работы с формулами могут значительно упростить процесс расчета.
Ошибки при расчете периметра ромба и как их избежать
Одна из наиболее распространенных ошибок при расчете периметра ромба - неправильное использование диагоналей. Периметр ромба вычисляется как сумма длин всех его сторон. Ошибкой является то, что многие люди включают диагонали в сумму сторон ромба, что приводит к завышенному значению периметра.
Чтобы избежать этой ошибки, необходимо помнить, что диагонали ромба не являются его сторонами. Диагонали - это отрезки, которые соединяют противоположные вершины ромба. Для расчета периметра ромба нужно знать длины его сторон, которые равны между собой.
Еще одной ошибкой является неправильное вычисление длин сторон ромба. Ромб имеет две диагонали, которые делят его на четыре равных треугольника. Длины сторон ромба можно выразить через длину его диагоналей, используя теорему Пифагора или теорему косинусов.
Ошибкой является также неправильное округление результатов вычислений. При вычислении периметра ромба необходимо соблюдать точность и округление до определенного числа знаков после запятой. Неправильное округление может привести к искажению результата и, как следствие, к ошибочным заключениям.
Для избежания ошибок при вычислении периметра ромба рекомендуется использовать точные и проверенные формулы, учитывать особенности ромба и правильно округлять результаты вычислений. Только при правильном использовании формул и методов можно достичь точности и достоверности результатов.