Ромб - это геометрическая фигура, у которой все стороны имеют одинаковую длину, а диагонали пересекаются под прямым углом.
Чтобы найти периметр ромба, можно использовать различные методы. Один из них - это использование длины диагонали.
Диагональ ромба - это прямая, соединяющая две противоположные вершины. Из свойств ромба следует, что диагонали делятся пополам и перпендикулярны друг другу.
Для нахождения периметра ромба через диагональ нужно умножить длину диагонали на 4. Так как диагонали делятся пополам, то можно воспользоваться формулой: P = d * 2 * √2, где P - периметр, d - длина диагонали.
Что такое периметр ромба?

Периметр ромба можно найти, зная длину одной его стороны. Так как все стороны ромба равны между собой, периметр можно вычислить как произведение длины стороны на 4.
Также периметр ромба можно найти, зная длину его диагонали. Для этого нужно умножить длину диагонали на 2 и найти квадратный корень из этого произведения, а затем умножить полученный результат на 2.
Например, если диагональ ромба равна 10 см, то периметр ромба будет равен 2 * √(10^2 + 10^2) = 2 * √(100 + 100) = 2 * √200 = 2 * 14.14 = 28.28 см.
Таким образом, периметр ромба - это длина его четырех сторон, которые равны между собой. Можно вычислить периметр ромба, зная длину одной его стороны или диагонали.
Ромб как особый вид четырехугольника
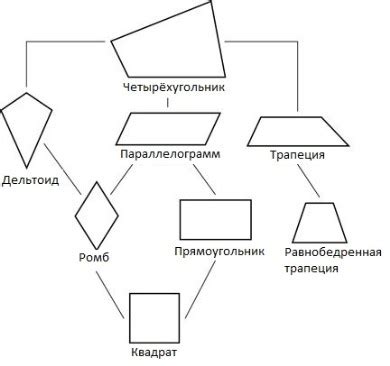
1. Все стороны ромба имеют одинаковую длину.
2. У ромба все углы равны между собой и равны 90 градусов каждый.
3. Диагонали ромба являются его осью симметрии: диагонали пересекаются под прямым углом и делят ромб на четыре равных треугольника.
4. Длины диагоналей ромба также равны между собой.
5. Площадь ромба можно вычислить, зная длину его диагоналей. Диагонали делят ромб на четыре равных треугольника, площади которых можно найти с помощью формулы S = (a * h) / 2, где a – длина основания треугольника (сторона ромба), h – высота треугольника (длина перпендикуляра, опущенного на основание треугольника).
6. Периметр ромба можно найти, зная длину его стороны, по формуле P = 4 * a, где a – длина стороны ромба.
Используя эти свойства ромба, можно эффективно решать задачи, связанные с вычислением его площади, периметра или других параметров.
Диагонали ромба и их связь с периметром

Диагонали ромба делят его на четыре равные треугольные фигуры. Каждая из этих фигур является прямоугольным треугольником, где диагональ является гипотенузой.
Таким образом, длина диагоналей ромба может быть использована для вычисления периметра. Периметр ромба равен двум удвоенным суммам длин его сторон. Так как все стороны ромба равны между собой, периметр можно представить как четыре раза длину одной из его сторон.
Когда известна длина одной из диагоналей, ее можно использовать для вычисления длины всех сторон ромба. Для вычисления периметра нужно просто умножить длину стороны на 4.
Формула для вычисления периметра ромба:
Периметр = 4 * длина стороны ромба
Таким образом, зная длину одной из диагоналей ромба, можно легко вычислить его периметр, используя простую формулу.
Как найти длину диагонали ромба?

Если известны длины сторон ромба, можно использовать теорему Пифагора для вычисления длины диагонали. Для этого нужно поделить ромб на два прямоугольных треугольника, в которых одна сторона равна половине одной диагонали.
Теорема Пифагора гласит, что в прямоугольном треугольнике с катетами a и b и гипотенузой c справедливо соотношение a^2 + b^2 = c^2.
Таким образом, для ромба с длинами сторон a и b длина диагонали c может быть найдена по формуле:
c = √(a^2 + b^2)
Например, если стороны ромба равны 4 и 5, то длина диагонали будет:
c = √(4^2 + 5^2) = √(16 + 25) = √41 ≈ 6.40
Таким образом, длина диагонали ромба равна приближенно 6.40.
Формулы для расчета длины диагонали через стороны или углы
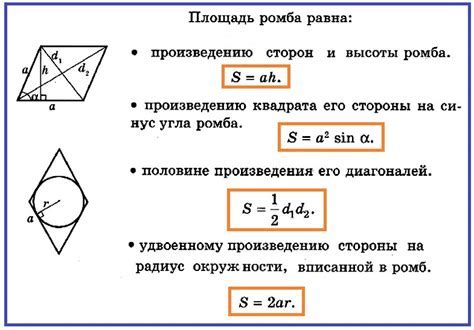
Если известны длины сторон ромба, можно использовать следующую формулу для расчета длины диагонали:
d = √(a² + b²)
где d - длина диагонали, a и b - длины сторон ромба.
Если известны значения углов ромба, можно воспользоваться следующей формулой для вычисления длины диагонали:
d = 2a sin(θ)
где d - длина диагонали, a - длина любой стороны ромба, θ - значение угла между двумя сторонами ромба.
Также можно использовать формулу для вычисления длины диагонали, если известны длины сторон и один из углов ромба:
d = (a² + b² - 2ab cos(θ))^(1/2)
где d - длина диагонали, a и b - длины сторон ромба, θ - значение угла между этими сторонами.
Иногда можно также использовать формулу диагонали через площадь ромба:
d = 2√(S)
где d - длина диагонали, S - площадь ромба.
С помощью этих формул вы можете легко вычислить длину диагонали ромба, имея доступные данные.
Примеры расчета длины диагонали ромба
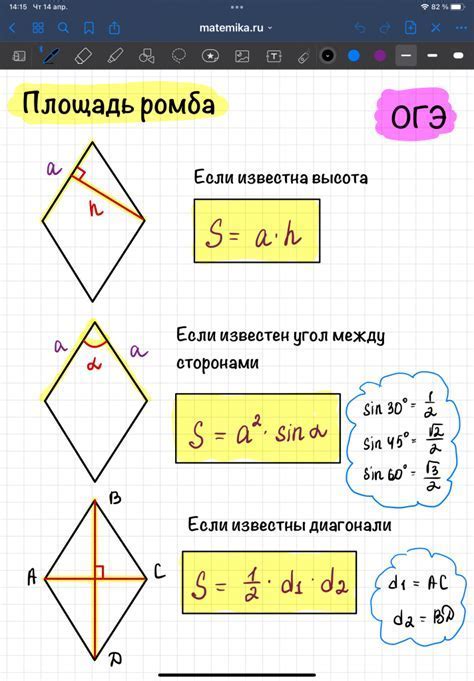
Длина диагонали ромба можно вычислить с помощью различных методов. Рассмотрим несколько примеров, чтобы лучше понять, как это делается:
| Пример | Значение стороны ромба (a) | Длина диагонали ромба (d) |
|---|---|---|
| Пример 1 | 5 | 7.07 |
| Пример 2 | 8 | 11.31 |
| Пример 3 | 10 | 14.14 |
Для расчета длины диагонали ромба можно использовать формулу:
d = a * √2
Где d - длина диагонали ромба, а - значение стороны ромба.
Таким образом, для каждого примера, можно получить значение длины диагонали ромба, используя формулу d = a * √2.
Как найти периметр ромба через его диагональ?

Периметр (P) ромба можно найти, зная длину его диагонали (d). Для этого нужно использовать формулу:
P = 4 * a, где а - длина стороны ромба.
Чтобы найти длину стороны ромба, необходимо знать длину диагонали (d) и применить следующую формулу:
a = sqrt((d^2)/2), где sqrt - квадратный корень.
Итак, чтобы найти периметр ромба через его диагональ, следует сначала рассчитать длину стороны ромба с помощью второй формулы, а затем умножить эту длину на 4 согласно первой формуле.
Связь диагоналей и периметра ромба
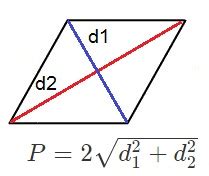
Периметр ромба можно выразить через длины его диагоналей. Пусть d1 и d2 - это длины диагоналей ромба. Тогда периметр P можно вычислить по формуле:
P = 4 * a = 4 * sqrt((d1/2)^2 + (d2/2)^2),
где a - длина стороны ромба.
Из этой формулы видно, что для нахождения периметра ромба необходимо знать лишь длины его диагоналей. Обратно, по известным стороным ромба можно вычислить длины его диагоналей следующим образом:
d1 = 2 * sqrt(a^2 + b^2),
d2 = 2 * sqrt(c^2 + b^2),
где a, b и c - длины сторон ромба.
Таким образом, диагонали и периметр ромба связаны между собой и можно использовать их вместе для нахождения различных параметров ромба.