Чтобы найти периметр сечения куба, необходимо сначала понять, что представляет собой сечение. Сечение - это плоскость, которая пересекает куб и образует фигуру на его поверхности. В данном случае, мы рассматриваем куб с ребром длиной 6.
Для того, чтобы найти периметр сечения, нужно определить форму фигуры, образованной пересечением. В данном случае, сечение куба происходит параллельно его ребру, поэтому фигура будет прямоугольником.
Чтобы найти периметр прямоугольника, необходимо сложить длины всех его сторон. В случае сечения куба с ребром 6, одна из сторон будет равна 6 (поскольку она совпадает с ребром куба), а вторая сторона будет равна длине пересечения двух ребер куба, то есть 6.
Таким образом, периметр сечения куба с ребром 6 составляет 24 (6 + 6 + 6 + 6). Имея эту информацию, можно строить дальнейшие расчеты и использовать ее для решения задач.
Определение периметра
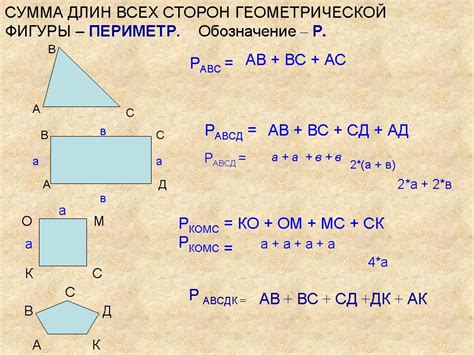
- Найдите длину одной стороны сечения. В случае с кубом это будет равно длине ребра куба, то есть 6.
- Умножьте длину одной стороны сечения на количество сторон сечения. В случае с кубом количество сторон сечения равно 4.
- Вычислите сумму полученных значений. В данном случае: 6 * 4 = 24.
Таким образом, периметр сечения куба с ребром 6 равен 24.
Сечение куба
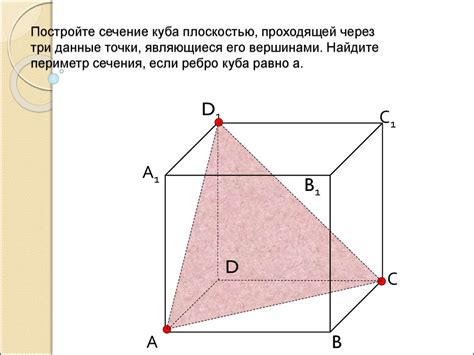
Сечения куба могут иметь разные формы и размеры в зависимости от ориентации плоскости и ее положения относительно куба. Сечение может быть кругом, овалом, прямоугольником, треугольником и так далее.
Для определения периметра сечения куба, необходимо вычислить сумму длин всех его сторон. Если сечение куба имеет форму прямоугольника, то периметр будет равен удвоенной сумме его двух сторон.
Например, если сечение куба имеет форму квадрата со стороной 4, то его периметр будет равен 4 + 4 + 4 + 4, то есть 16.
Таким образом, периметр сечения куба зависит от его формы и размеров и может быть вычислен путем суммирования длин его сторон или применения соответствующей формулы, основанной на типе сечения.
Геометрическое представление
Геометрическое представление сечения куба с ребром 6 может быть представлено следующим образом.
- Рассмотрим плоскость, которая проходит через середины противоположных ребер куба.
- Эта плоскость разделит куб на две одинаковые половинки.
- Внешний вид сечения зависит от ориентации плоскости относительно ребер куба.
Для примера, если плоскость проходит горизонтально, то сечение будет иметь форму прямоугольника со сторонами, равными ребру куба (6).
Если плоскость проходит вертикально, то сечение будет иметь форму квадрата со сторонами, равными диагонали грани куба. Диагональ грани куба можно найти с помощью теоремы Пифагора: √(6^2 + 6^2) = √(72) ≈ 8.49.
Таким образом, геометрическое представление сечения куба с ребром 6 зависит от ориентации плоскости и может быть прямоугольником или квадратом.
Способы нахождения периметра

1. Поскольку куб имеет пять граней, периметр сечения будет равен длине стороны грани. В данном случае, длина стороны грани куба равна 6, поэтому периметр сечения будет также равен 6.
2. Другой способ нахождения периметра сечения - это умножить длину стороны грани на количество сторон сечения. В случае с кубом, это будет равно 6 * 4 = 24. Однако, поскольку все ребра имеют одинаковую длину, можно просто взять длину одного ребра и умножить на количество сторон сечения, что даст тот же результат - 6 * 4 = 24.
| Способ | Периметр |
|---|---|
| По длине стороны грани | 6 |
| По формуле: длина стороны грани * количество сторон сечения | 24 |
Куб с ребром 6

В данном случае рассматривается куб с ребром 6. Это означает, что каждая сторона куба имеет длину 6 единиц.
Периметр – это сумма длин всех сторон фигуры. Для куба с ребром 6 периметр сечения можно найти следующим образом:
1. Найдем площадь сечения куба. Так как все грани куба – квадраты, площадь одной грани равна квадрату длины стороны. В случае куба с ребром 6, площадь одной грани будет равна 6 * 6 = 36 единицам квадратным.
2. Для нахождения периметра сечения необходимо найти периметр полученной площади. Поскольку сечение куба является квадратом, его периметр равен четырехкратному значению стороны. В данном случае периметр сечения будет равен 4 * 6 = 24 единицам.
Таким образом, периметр сечения куба с ребром 6 будет равен 24 единицам.
Характеристики куба
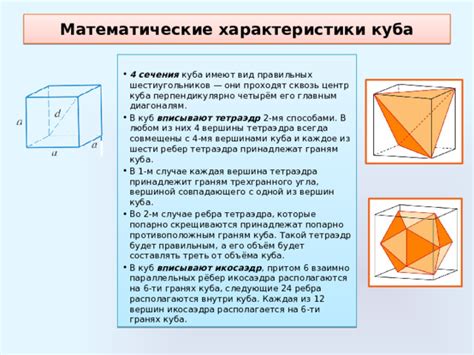
Основные характеристики куба:
- Ребро: длина каждого ребра куба одинакова и определяет размеры фигуры. В данном случае, ребро куба равно 6 единицам.
- Площадь грани: площадь каждой грани куба равна квадрату длины его ребра. В данном случае, площадь грани составляет 36 квадратных единиц.
- Объем: объем куба вычисляется как куб длины его ребра. В данном случае, объем куба равен 216 кубическим единицам.
- Периметр сечения: периметр сечения куба - это периметр самого сечения, то есть окружности. Для куба с ребром 6 единиц периметр его сечения составит 12π единиц.
Характеристики куба позволяют определить его размеры, объем и другие геометрические свойства. Знание этих характеристик важно при решении задач и анализе геометрических фигур.